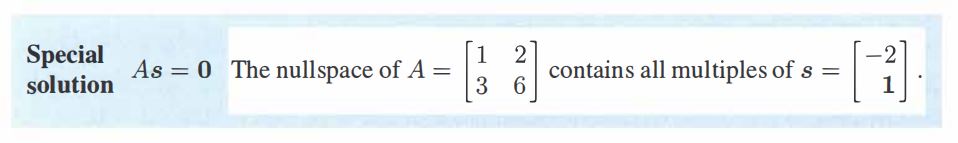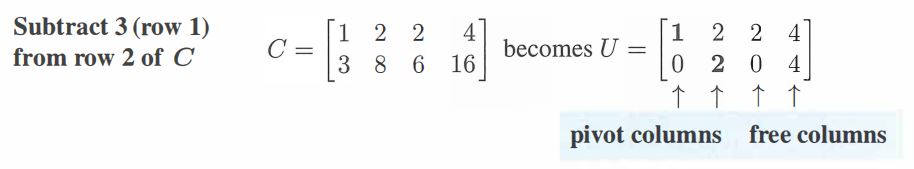L1

Def 2: 点乘 Dot Product $x\cdot y=x^T y=\sum_{i=1}^n x_i y_i$
$x\cdot y=y\cdot x$
For $x,y\in\mathbb{R}^n$, 但对于 $x,y\in \mathbb{C}^n$ 点乘的定义将变化

Def 3: 范式 Norm \(\|x\|=(\sum_{i=1}^n|x_i|^2)^{1/2}=(x\cdot x)^{1/2}\)

L2

2.1 Lines on $\mathbb{R}^2$

$L$ is a line if stasify \(L=\{(x,y):ax+by=c\}\)

where, $\vert a\vert+\vert b\vert\neq 0$

Examples

1. $x=1,\;L={(1,y),y\in\mathbb{R}}$
2. $y=x+1,\;L={(x,x+1),x\in\mathbb{R}}$

2.2 Lines and planes on $\mathbb{R}^3$

\(P=\{(x,y,z)\in\mathbb{R}^3:ax+by+cz=d\}\)

where,

• $eq_1=a_1x+b_1y+c_1z=d_1$
• $eq_2=a_2x+b_2y+c_2z=d_2$

2.3 Hyperplane

Consider the dimensions

1. $\mathbb{R}^3\to \text{dimension } 3\to 3D$
2. $\text{planes in }\mathbb{R}^3\to 2D$
3. $\text{lines in }\mathbb{R}^2\text{ and }\mathbb{R}^3\to 1D$

Then we define hyperplane

where,

• $P$ has dimension $n-1$
• $\textbf{a}\in\mathbb{R}^n,\;b\in \mathbb{R}$

2.4 Multidemensional system

\(\textbf{A}\textbf{x}=\textbf{b}\to\begin{cases} & a_{11}x_1+...+a_{1n}x_n=b_1\\ & ......\\ & a_{m1}x_1+...+a_{mn}x_n=b_m \end{cases}\) where, \(\textbf{A}=\begin{bmatrix} a_{11} & a_{12} & ... & a_{1n} \\ a_{21} & a_{22} & ... & a_{2n} \\ ... & ... & ... & ... \\ a_{m1} & a_{m2} & ... & a_{mn} \end{bmatrix},\textbf{b}=(b_1,...,b_m)^T,\;\textbf{x}=(x_1,...,x_n)^T\)

令 $\tilde{a}k=(a{k1},…a_{km})\in\mathbb{R}^n$ 由此可得 $m$ 个超平面 $H_k$ \(H_k=\{x\in\mathbb{R}^n:\tilde{a}_k \textbf{x}=b_k\}\to\begin{cases} & H_1:\tilde{a}_1 \textbf{x}=b_1\\ & ......\\ & H_m:\tilde{a}_m \textbf{x}=b_m \end{cases}\)

dimension of $H_k=n-1$

Solution of system $x\in\cap_{k=1}^mH_k$

1. when $x\in\cap_{k=1}^mH_k$ is empty: no solution
2. many solutions
3. single solution

例如当 $m=2,\;n=3$（三维空间中的两个面），除了两面不相交时没有解之外，还可能有直线解或者平面解（这里的 many solutions 由于涉及到高维空间，没有必要从几何的角度理解，只要把它看做是矩阵有多个解就行了）

2.5 Elimination

\(\begin{pmatrix} 3 & 2 & 1& |&39 \\ 2 & 3 & 1& |&34 \\ 1 & 2 & 3& |&26 \end{pmatrix} \xrightarrow[l_{21}=\frac{2}{3}]{(2,1)} \begin{pmatrix} 3 & 2 & 1 & |&39 \\ 0 & \frac{5}{3} & \frac{1}{3}& |&8 \\ 1 & 2 & 3& |&26 \end{pmatrix} \xrightarrow[]{}...\xrightarrow[]{} \begin{pmatrix} 3 & 2 & 1& |&39 \\ 0 & \frac{5}{3} & \frac{1}{3}& |&8 \\ 0 & 0 & \frac{12}{5}& |&\frac{33}{5} \end{pmatrix}\) where,

1. $(2,1)$ 表示第二行减去第一行
2. $l_{21}=\frac{2}{3}$ 表示 $l_2-\frac{2}{3}l_1$

2.6 Operations Counting

每次高斯消元过程均由相同数量的乘法以及减法操作组成 对于 $n\times n$ 的矩阵 \(\begin{pmatrix} x & x & ... & x \\ x & x & ... & x \\ ... & ... & ... & ... \\ x & x & ... & x \\ \end{pmatrix}\)

第一次高斯消元需要进行 $n(n-1)$ 步的乘法以及减法操作，后转换成如下矩阵 \(\begin{pmatrix} x & x & ... & x \\ 0 & x & ... & x \\ ... & ... & ... & ... \\ 0 & x & ... & x \\ \end{pmatrix}\)

随后第二次、第三次……直至最后一次高斯消元，各需要进行 $(n-1)(n-2),(n-2)(n-3)$…步的操作，由此 \(\text{Total Operations} =\sum_{k=2}^n k(k-1)=\frac{n^3-n}{3}\approx n^3\)

L3

3.1 Matrix Calculation Rules

(1) $(AB)^T=B^TA^T$

(2) $ABC=(AB)C=A(BC)$

(3) $(AB)^{-1}=B^{-1}A^{-1}$

(4) $(A^T)^{-1}=(A^{-1})^T$

3.2 Matrix Inverse

Defined only for square matrices The unit matrix $I$ satisfy \(IA=AI=A,\;\text{for any }A\)

(1) If $A$ has inverse $A^{-1}$, then it is unique

(2) Let $A\in\mathbb{C}^{n\times n},x\in\mathbb{C}^n$. If there exist $A^{-1},\;s.t.\;Ax=0$, then $x=0$

(3) If there exist $x\in\mathbb{C}^n, x\neq 0$ that let $Ax=0$, then $A$ cannot have inverse (is singular)

这些概念中，2、3 两点可以从线性变换矩阵的角度来理解（详见 Some Math Concepts Section 2.3.1）

3.3 Calculation of inverse

Solving $A^{-1}$ is equal to solve $X$ in the following problem \(AX=I\)

Use Gauss Elimination: \((A|I)\to (I|A^{-1})\)

Example \(A=\begin{bmatrix} 1 & 3 \\ 2 & 7 \end{bmatrix}\)

当然，对于 $2\times 2$ 矩阵可以直接写出其逆矩阵 \(A^{-1}=\frac{1}{ad-bc}\begin{pmatrix} d & -b\\ -c & a \end{pmatrix}\)

3.4 Permutation matrix

\(P_{ij} \in \R^{n\times n}\text{ is obtained from }I\text{ by switching }i_{th}\text{ and }j_{th}\text{ rows}\) \(P_{23}=\begin{bmatrix} 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \end{bmatrix}\)

Properties

1. $P_{12}=P_{12}^{-1}=P_{21}$
2. $P_{31}P_{21}\neq P_{21}P_{31}$

3.5 Elimination matrix

$\text{Let } A\in\mathbb{C}^{n\times n}\text{ be given}$ $E_{ij}$ is the matrix such that $E_{ij}A$ means \(i_{th}\text{ row} - l_{ij}\times j_{th}\text{ row}\) where $l_{ij}=\frac{a_{ij}}{a_{jj}}$ 相当于 \((a_{i1},...,a_{in})-(a_{j1},...,a_{jn})\times \frac{a_{ij}}{a_{jj}}\)

Example \(A=\begin{bmatrix} 3 & 1 \\ 1 & 0 \end{bmatrix}\to E_{21}A=\begin{bmatrix} 3 & 1 \\ 0 & -\frac{1}{3} \end{bmatrix}\to E_{21}=\begin{bmatrix} 1 & 0 \\ -\frac{1}{3} & 1 \end{bmatrix}\)

3.6 Triangular Mtrices

set $U$ represent upper triangular matix, satisfying $u_{ij}=0,\;i<j$ set $L$ represent lower triangular matix, satisfying $l_{ij}=0,\;i<j$

Property n 个上三角矩阵的乘积仍为上三角矩阵（下三角同理） 即 $\text{If } L_1,…,L_n \in L,\;\text{then }(L_1L_2…L_n)\in L$

3.7 LU-Decomposition

aka. LU-Factorization

3.7.1 Definition

并不是所有矩阵都能被 LU 分解，例如 \(\begin{bmatrix} 0 & 1 \\ 1 & 1 \end{bmatrix}\)

但是可以通过构造一个 Permutaion Matrix $P$ 使得任何 $A\in\mathbb{C}^{n\times n}$ 都能被 LU 分解

3.7.2 Find P, L, U from A

1. From $A\to U:U=E_{n(n-1)}E_{n(n-2)}E_{(n-1)(n-2)}…E_{32}E_{n1}…E_{31}E_{21}A=EA$
2. Then $A=E^{-1}U=LU$
3. Therefore, $L=E^{-1}$ (if need $P$, similarly, $U=EPA,\;PA=E^{-1}U=LU$)

LU-factorization is not unique, since $P$ is not unique (不同的换行方式会使得 $PA$ 变得不同)

3.7.3 Lemma

1. $A\in\mathbb{C}^{n\times n}$ is invertible $\iff$$\forall\;b\in\mathbb{C}^n,\exist\;x\in\mathbb{C}^n$ satisfy $Ax=b$

• Proof: 左到右好证（$x=A^{-1}b$）
  右到左，可令 $b_1,…,b_n$ 为 $n$ 个标准基向量，例如 $b_1=[1,0,…,0]^T,b_2=[0,1,…,0]^T$

2. $A$ is singular $\iff U$ has zero element on diagonal

• Proof: 不需要证明，存在零元素就意味着存在 free column

3.7.4 Use LU-Decomposition to solve $Ax=b$

\(Ax=LUx=b\to Ly=b,Ux=y\)

L5: Vector spaces, Subspaces

In this lecture, we consider vector spaces over the field $E$ ($E=\R\text{ or }\Complex$)

5.1 Subspace

Let $X$ be a vector space, and $Y\subset X$. We say that $Y$ is a subspace of $X$ if $Y$ is closed to addition and multiplication on scalars ($Y$ 对加法和乘法封闭) \(\text{If }\begin{cases} x,y\in Y &\text{then } x+y\in Y \\ \alpha\in E,x\in Y &\text{then } \alpha x\in Y \end{cases}\)

Any subspace contains zero space

Ex: (1) $Y$ is not a subspace of $X$ if $X=E=\Complex,Y={x\in X:\text{Im}(x)=0}$. Since when $x=1\in Y,i*x\notin Y$

(2) 三维空间中的一个经过 $(0, 0, 0)$ 点平面是 $\R^3$ 的子空间（注意！该平面并不是 $\R^2$，只能说是 $2D$）

5.1.1 Lemma

1. For any two subspaces $Y,Z$ of a vector space $X$, $Y\cap Z$ is also a subspace of $X$ proof: let

1. $Y-Z$ is also a subspace of $X$ 证明类似
2. $Y\cup Z$ is not a subspace of $X$ 例如 $Y={(0,\R)},Z={(\R,0)}\to Y\cup Z={(x,y)|xy=0}$，但是 $(1,1)=(1,0)+(0,1)$ 并不在其中

5.2 Span

Let $X$ be a vector space, and $S\subset X$. Define the span of $S$ as the set of all linear combinations of vectors from $S$ (denote: $\text{span}(S)$)

Lemma

For any set $S\subset X$, $Y=\text{span}(S)$ is a subspace of $X$

Example

Let $p,q\in\R^2$. What is the span of $S={p,q}$?

Let $p=\begin{pmatrix} p_1 \ p_2 \end{pmatrix},q=\begin{pmatrix} q_1 \ q_2 \end{pmatrix}$, then $y=\alpha_1 p + \alpha_2 q=\begin{pmatrix} p_1 & q_1 \ p_2 & q_2 \end{pmatrix}\begin{pmatrix} \alpha_1 \ \alpha_2 \end{pmatrix}$ Therefore if $p_1q_2\neq p_2q_1$, then $\text{span}(S)=\R^2$

5.3 Column space: $C(A)$

For matrix $A_{m\times n}$, column space $C(A)$ consists of all linear combinations of the columns, which is a subspace of $\R^m$ \(C(A)=\text{span}\{a_i\}\)

Solving $Ax=b$ 即用列的组合去表示 $b$。因此，$Ax=b$ is solvable iff $b\in C(A)$

Theorem For matrix $A\in E^{n\times n}$, the following three statements are equivalent：

1. $A$ 可逆
2. $N(A)={0}$
3. $C(A)=E^n$

5.4 Null space: $N(A)$

Define $A$ is a $m\times n$ matrix

5.4.1 Def

$N(A)$ consists of all solutions to $Ax= 0$, where $x\in \R^n$, $N(A)$ is a subspace of $\R^n$（注意！此处的维度与 $C(A)$ 不同）

Example When $A=[1\;2\;3]$, $N(A)$ 即为垂直于向量 $(1,2,3)$ 的平面

5.4.2 Special solution

如何求得 special solutions?

1. 首先通过高斯消元找到 pivot columns & free columns
2. 有几个 free columns 就有几个 special solutioins $C$ 包含两个，因此设 $s_1=\begin{pmatrix} a_1
   b_1
   1
   0 \end{pmatrix},s_2=\begin{pmatrix} a_2
   b_2
   0
   1 \end{pmatrix}$ 即分别将一个 free column 的值设为 $1$，其他 free columns 的值设为 $0$，分别代入 $Us=0$ 求 $a_1,…,a_n,b_1,…,b_n,…$，最后可得

5.4.3 The Reduced Row Echelon Form: $R$

将矩阵 $U$ 进一步进行如下消元得到矩阵 $R$

1. Use pivot rows to eliminate upward in $R$
2. Divide the whole pivot row by its pivot，即让 pivit = 1

记做 $R=\text{reff}(A)$，满足 \(N(A)=N(U)=N(R)\)

$C(A)$ consists of all vectors of the form $(b_1,b_2,b_3,0)$

L6 Solution of equation $Ax=\bf{b}$

6.1 Linear manifolds

A linear manifold is a linear subspace that has possibly been shifted away from the origin. \(\text{Let }X\text{ be a vector space},\;a\in X,\;Y\text{ is a subspace of }X \newline \text{Then }a+Y\text{ is a linear manifold}\)

例如在 $\R^2$ 空间中，linear manifolds 可以是点、线或者 $\R^2$ 自身

其他部分详见 Chapter3

L7

Independence, basis, dimension

7.1 Dimension of a sum of subspaces

Let $X$ be a vector space, $Y$ and $Z$ be a subspaces.

Def 1: Sum of subspaces

\(Y+Z=\lbrace y+z,y\in Y, z\in Z\rbrace\)

Fact 1: $Y+Z,Y\cap Z$ are also subspaces, while $Y\cup Z$ is not

Theorem 1: \(\text{dim}(Y+Z)=\text{dim}(Y)+\text{dim}(Z)-\text{dim}(Y\cap Z)\)

7.2 Base in $\mathbb{E}^n$

Theorem 1: If $u_1, …., u_n$ and $v_1, …., v_n$ are two bases in $\mathbb{E}^n$ then there exists an invertible matrix $B \in \mathbb{E}^{n\times n}$ such that \(UB=V\)

Theorem 2.1: Let $A \in \mathbb{E}^n$ be invertible. If $u_1, …., u_n$ is a basis in $\mathbb{E}^n$, then $Au_1, …., Au_n$ is also a basis in $\mathbb{E}^n$.

Theorem 2.2: Let $A \in \mathbb{E}^{n\times n}$ be invertible. If $u_1, …., u_n$ is a basis in $\mathbb{E}^n$, then $u_1A, …., u_nA$ is also a basis in $\mathbb{E}^n$.

• Proof: (For Theorem 2.1) Let $b\in \mathbb{E}^n$, then $A^{-1}b\in \mathbb{E}^n$, then express \(A^{-1}b=\sum c_ku_k\to b=A(A^{-1}b)=\sum c_k(Au_k)\)

Similar for Theorem 2.2

7.2.1 How to find if $\lbrace u_1,…,u_n\rbrace\subset \mathbb{E}^n$ is a basis

The rule: Compose a matrix using $\lbrace u_1, …, u_n\rbrace$ as columns (or, alternatively, as rows). The set $\lbrace u_1, …, u_n\rbrace$ is a basis iff $A$ is invertible. Since Gauss-Jordan elimination procedure means multiplication on an invertible matrix, we can apply Gauss- Jordan elimination procedure to test matrix invertibility.

7.2.2 Infinite dimensional spaces

略，好像课件里没讲到啥内容

L8

Four fundamental subspaces defined by a matirx

按照老师课件的要求，对 $R$ 得再进行一波换列操作，使得 \(R=\begin{pmatrix} I & F \\ 0_{(m-r)\times r} & 0 \end{pmatrix}\)

注意交换列之后自变量的顺序也要做对应的交换，例如交换 $2,3$ 列之后 $(x_1,x_2,x_3)\to(x_1,x_3,x_2)$

8.1 Dimension of linear manifolds

Def 1: Linear manifold

If $X$ is a linear space, $Y$ is a subspace, $a\in X$, $M = a + Y$ is a linear manifold, then we say that $\text{dim}(M) = \text{dim}(Y)$.

Corollary 1: Let $A\in E^{m\times n}$, $b\in E^n$. For a linear system $Ax = b$, all solutions $x\in E^n$ form a linear manifold \(x_{part}+N(A)\)

in $E^n$ that has dimension $n-\text{rank}(A)$ ($x_{part}$ is the particular solution)

8.1.1 Lines and planes in $\mathbb{R}^3$

Ex.1: For any nonzero $a\in \mathbb{R}^3$ and $b\in \mathbb{R}$, let $Y = \lbrace x\in\mathbb{R}^3 : a^Tx = b\rbrace$. Find $Y$ and $\text{dim}(Y)$

1. $A=a^T$, then we get $Y=x_{part}+N(A)$
2. Since $m=1,n=3,\text{rank}(A)=1$, $\text{dim}(Y)=\text{dim}(N(A))\to Y$ is a plane

Ex.2: For $A\in\mathbb{R}^{3\times 3}$ and $b\in\mathbb{R}^3$, let $Y = \lbrace x\in\mathbb{R}^3 : Ax = b\rbrace$. Find $Y$ and $\text{dim}(Y)$

1. If $\text{rank}(A)=3$, $Y=x_{part}$, $\text{dim}(Y)=0$
2. If $\text{rank}(A)=2$, $Y=x_{part}+N(A)$, $\text{dim}(Y)=1$, is a line
3. If $\text{rank}(A)=1$, $Y=x_{part}+N(A)$, $\text{dim}(Y)=2$, is a plane

8.2 Linear Transformations

Definition: Define mapping $T:X\to Y$ is linear iff \(\begin{aligned} T(\alpha x)&=\alpha T(x),\forall \alpha\in E,x\in X \\ T(x+y)&=T(x)+T(y),\forall x,y\in X \end{aligned}\)

将 $T$ 称之为 linear transformation/ linear mapping/ linear operator/ linear function，常常用 $Tx$ 指代 $T(x)$

Ex.1: Linear transformations

1. $X=\mathbb{E}^n,Y=\mathbb{E}^m\to T(x)=Ax\;\;\;(A\in \mathbb{E}^{m\times n})$
   
2. $X=\mathbb{E}^{n\times n},Y=\mathbb{E}^{n\times n}\to T(x)=MxN\;\;\;(M,N\in X)$
   
3. $X=Y=\text{span}(1,t,t^2,…)\to T(x)=\frac{dx}{dt}$
   
4. $X=Y=\mathbb{C}\to T(x)=\text{Re}(\mathbb{C})$
   
5. $X=\text{span}(1,t,t^2,…),Y=\mathbb{R}\to T(x)=x(0)+\int_0^{10}(2x(t)+5)dt$

Ex.2: Not linear

1. $X=Y=\mathbb{R}\to T(x)=x+1$, not linear since $T(0\cdot x)\neq0\cdot T(x)=0$
   

2. $X=Y=\mathbb{R}\to T(x)=

   x

   $

8.2.1 Matrices of linear transformations: general case

Theoerm: Let $T:X\to Y$ is a linear transformation from vector spaces $X$ and $Y$ with bases $\lbrace u_j\rbrace$ and $\lbrace v_k\rbrace$ respectively. Let $\lbrace a_{ij}\rbrace$ be the set of coordinates for $T(u_j)$ in the basis $\lbrace v_k\rbrace$, and let matrix $A$ be formed as $A = \lbrace a_{ij}\rbrace$. Then \(T(x)=y\text{ iff } Ac=d\)

where $c$ is the vector column of x in the basis $\lbrace u_j\rbrace$, $d$ is the vector column of y in the basis $\lbrace v_k\rbrace$

关于 $u,k,c,d,A$ 的维度

1. 令 $X\in \mathbb{E}^n, Y\in \mathbb{E}^m$，因此 $u_j\in \mathbb{E}^n, v_k\in \mathbb{E}^m$
2. 再令 $\text{dim}(\lbrace u_j\rbrace)=p$，即 $X$ 有 $p$ 个 bases 同时 $\text{dim}(\lbrace v_k\rbrace)=q$，即 $Y$ 有 $q$ 个 bases 因此 $c\in \mathbb{E}^p, d\in \mathbb{E}^q$，验证： $x_{n\times 1}=\lbrace u_j\rbrace_{n\times p}\times c_{p\times 1}$
3. 注意，这里的 $A$ 并不是 $Ax=y$ 的变换矩阵，而通过 $Ac=d$ 易得 $A\in \mathbb{E} ^{q\times p}$

理解 $T(x)=y\text{ iff }Ac=d$ 如果用一个公式来联系 $T(x)=y$ 与 $Ac=d$， \(T(x)=T(\lbrace u_j\rbrace\times c)=\lbrace v_k\rbrace\times Ac=\lbrace v_k\rbrace\times d=y\)

具体示例详见以下两个示例

Ex 1: Let $X=\text{span}\lbrace 1, t, t^2\rbrace$, $Y=\text{span}\lbrace 1, t\rbrace$ and the ransform $T=\frac{dx}{dt}$, find the matrix of tranform $T$ \(\dim({u_j})=3,\dim({v_k})=2 \to c_{3\times 1}, d_{2\times 1}\to Ac=d \to A_{2\times 3}\)

由于 $A$ 的第 $i$ 列相当于把 $\lbrace v_k\rbrace$ 转换成 $T(u_i)$ ，因此可得 \(\begin{aligned} T(u_0)&=0=0\cdot v_0+0\cdot v_1 \\ T(u_1)&=1=1\cdot v_0+0\cdot v_1 \\ T(u_2)&=2t=0\cdot v_0+2\cdot v_1 \\ \end{aligned} \to A=\begin{bmatrix} 0 & 1 & 0 \\ 0 & 0 & 2 \end{bmatrix}\)

Ex 2: Let $X=\text{span}\lbrace(2,3,1)^T,(1,0,0)^T\rbrace$, $Y=\mathbb{R}$ and the ransform $T(x)=x_1+x_3,x=(x_1,x_2,x_3)^T$, find $A$ \(\begin{aligned} T(u_0)&=3=3\cdot 1 \\ T(u_1)&=1=1\cdot 1 \end{aligned}\to A=\begin{bmatrix} 3 & 1 \end{bmatrix}\)