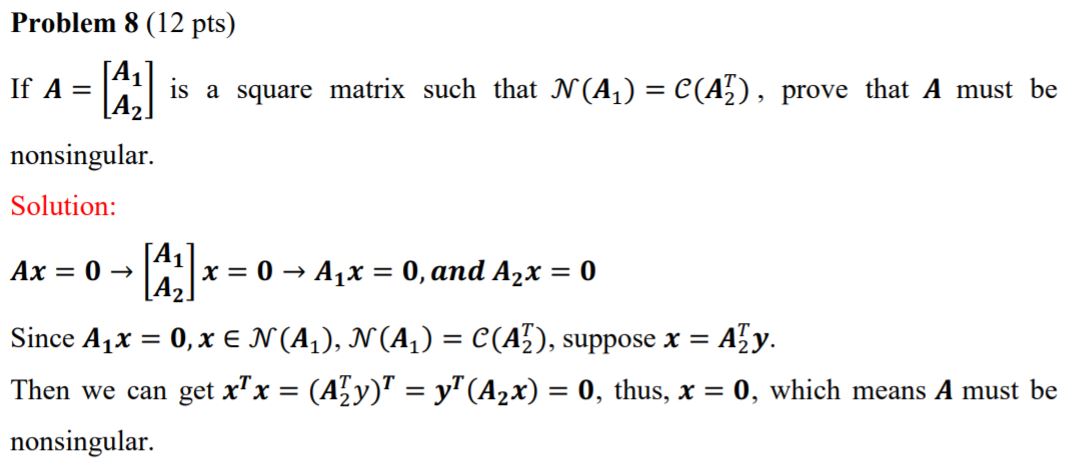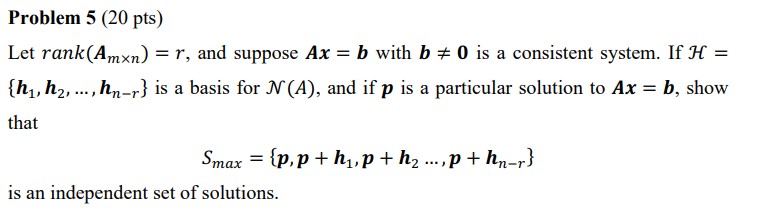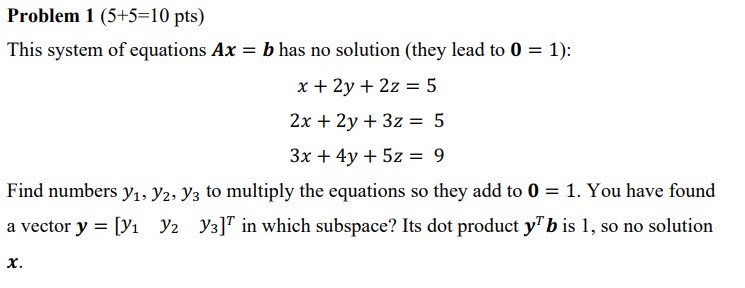DH1

1.1 Schwarz Inequality

\(\|\bf{w}\|\geq(\bf{v}\cdot\bf{w})/\|\bf{v}\|\)

1.2 Linearly Independent

Definition $\text{Let }x_1,…,x_n \in \R^n, \text{we say that they are linearly independent if, for any }c_1,…,c_n \in \R, \text{if } \sum_{i=1}^n c_ix_i=0 \text{ then } c_i=0 \text{ for all } i$

根据这一定义，使用反证法可得： $\text{If }x_1=0\;(i.e\;|x_1|=0),\text{ then the system }x_1,…,x_n\in\R^n \text{is not independent}$ (因为当 $c_1=1,c_i=0,i>1$ 时, 满足 $\sum c_ix_i=0$, 却不满足 $c_i=0 \text{ for all } i$)

1.3

Let $x_1,x_2,x_3$ 为矩阵 $X$ 的列向量，且有 $Ax_1=b_1,Ax_2=b_2,Ax_3=b_3$ 则 \(AX=[Ax_1,Ax_2,Ax_3]=[b_1,b_2,b_3]\)

DH2

2.1

If $A$ if a square matrix such that $I-A$ is nonsingular, prove that \(A(I-A)^{-1}=(I-A)^{-1}A\)

已知等式 $A(I-A)=(I-A)A$ 恒成立, 对于等式两边的两边都乘上 $(I-A)^{-1}$，可得 \((I-A)^{-1}A(I-A)(I-A)^{-1}=(I-A)^{-1}(I-A)A(I-A)^{-1}\)

2.2

可以用高斯消元的方式来求逆矩阵 $AA^{-1}=I$，即 \([A\;|\;I]\to[I\;|\;A^{-1}]\)

也可以用来求解 $AX=B$ \([A\;|\;B]\to[I\;|\;X]\)

若是求解 $XA=B$, given $A,B$, 不妨先观察一下 $A,B$ 两者间是否存在关系 (是否可以通过 elimination or permutation 由 $A$ 得到 $B$)

2.3

2.4 LU Factorization

1. 计算 $L=E^{-1}$ 时, 一个一个把 $E_{ij}^{-1}$ 乘起来就行 (将 $E_{ij}$ 非对角元素取负即可得到 $E_{ij}^{-1}$)
2. 使用 $PA=LU$ 辅助计算 $Ax=b$ 时, 记得 $b$ 也要进行对应的置换 \(Ax=b\to LUx=Pb\)

DH3

3.1 If a subspace

1. 在判断某一集合是否为 subspace 时，首先可以检查一下该集合是否存在 0，如果不存在，直接否定。(例如 ${x

   Ax=b,\text{where }A_{m\times n}\neq 0\text{ and }b_n\neq 0}$ 显然不是一个 subspace)

2. 然后再判断其余两个条件是否也同时满足 \(\text{If }\begin{cases} x,y\in Y &\text{then } x+y\in Y \\ \alpha\in E,x\in Y &\text{then } \alpha x\in Y \end{cases}\)

3.2

这道题的解法真的很妙，

1. $A$ is nonsingular: \(Ax=0 \iff x = 0\)
2. \[Ax=0\to \begin{bmatrix} A_1\\ A_2 \end{bmatrix}x=0\]
3. \[\begin{cases}x\in N(A_1) \\N(A_1)=C(A_2^T)\end{cases}\to \exist\;y\neq 0,s.t.\;x=A^T_2y\]
4. \[x^Tx=(A^T_2y)^Tx=y^T(A_2x)\]

由于 $y\neq 0$, $x^Tx=0$ 当且仅当 $x=0$

3.3 If $b\in C(A)$

$b\in C(A)$ 的充要条件为 $Ax=b$ 有解

3.4

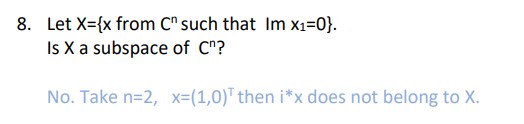
当 $x\in \mathbb{C}^n$ 时, 其 mutiplication on scalars 也可以乘以虚数

DH4

4.1

T/F: A vector space has infinitely many different bases

False (counter example: $V={0}$) 不要忘了零空间啊

4.2

To show $S_{max}$ is linearly independent, suppose \(0=\alpha_0p+\sum_{i=1}^{n-r}\alpha_i(p+h_i)=(\sum_{i=0}^{n-r}\alpha_i)p+\sum_{i=1}^{n-r}\alpha_ih_i\)

两边同乘 $A$, 由于 $Ah_i=0,Ap=b$, 可得 \((\sum_{i=0}^{n-r}\alpha_i)b=0\to\sum_{i=0}^{n-r}\alpha_i=0\)

再代回原式, plus that ${h_i}$ independent, 可得 \(0=\sum_{i=1}^{n-r}\alpha_ih_i\to a_i=0\)

Therefore, we can conclude that the only solution to $0=\alpha_0p+\sum_{i=1}^{n-r}\alpha_i(p+h_i)$ is $a_i=0$, and then $S_{max}$ is an independetn set

DH5

5.1

看一下 Chapter-10

DH6

6.1

$y$ should be in $N(A^T)$, but not $N(A)$. 零空间意味着 $Ay$ 把每个等式的左边变成 0, 况且这时候求的应该是 $[x,y,z]$, 因此不符合要求

而左零空间则能够吧矩阵每列的和变成 0, 例如 $y_1(x)+y_2(2x)+y_3(3x)=0$, 这样就满足了题目要求 “so that they add to $0=1$”. 求出左零空间的 base 之后, 再乘上一个常数使等号右侧加起来等于 $1$ 即可

6.2

当两个投影矩阵的投影空间存在包含关系时, 即先投到小的在投到大的, 只要算出投小的即可

6.3 QR Factorization

\(A=QR\)

对于矩阵 $A=[a_1,a_2,a_3],{a_i}$ independent, 使用 Gram-Schmidt process 由相互独立的 ${a_i}$ 生成标准正交矩阵 $Q=[q_1,q_2,q_3]$

由于 $Q^{-1}=Q^T$, 因此 $R=Q^TA$

注意: 虽然 QR 是一种矩阵分解方式, 但这并不意味着在算 least squares problem $Ax=b$ 时, 以下公式 2 就一定比公式 1 好用, 往往还是直接用公式 1 比较简单粗暴 \(\tag{1} \hat{x}=(A^TA)^{-1}A^Tb\)

DH7

7.1 Skew-symmetric matrix

\(A^T=-A\)

DH8

8.1

Find the eigenvectors from \(A-3I=\begin{bmatrix} 0 & 0 & 0\\ 0 & 1 & -1\\ 0 & 1 & -1 \end{bmatrix}\)

在上次遇到这种情况, 作者”很自然”地直接算出来了一个 $x=[1,1,1]^T$, 大错特错!!! 从 free columns 的角度看, 两个 free columns 意味着两个特征向量 $x_1=[1,0,0]^T,x_2=[0,1,1]^T$

DH9

9.1 Diagonalizable matrix

判定方式详见 Chapter-06.2

DH10

10.1

这道题挺神奇的, 原理不是很懂. 但是就结果来看, 特征值中的 max 与 min 等同于 $\frac{x^TSx}{x^Tx}$ 的 max 与 min

10.2

对于 $A=U\Sigma V^T$, $u_i\in C(A),v_i\in C(A^T)$