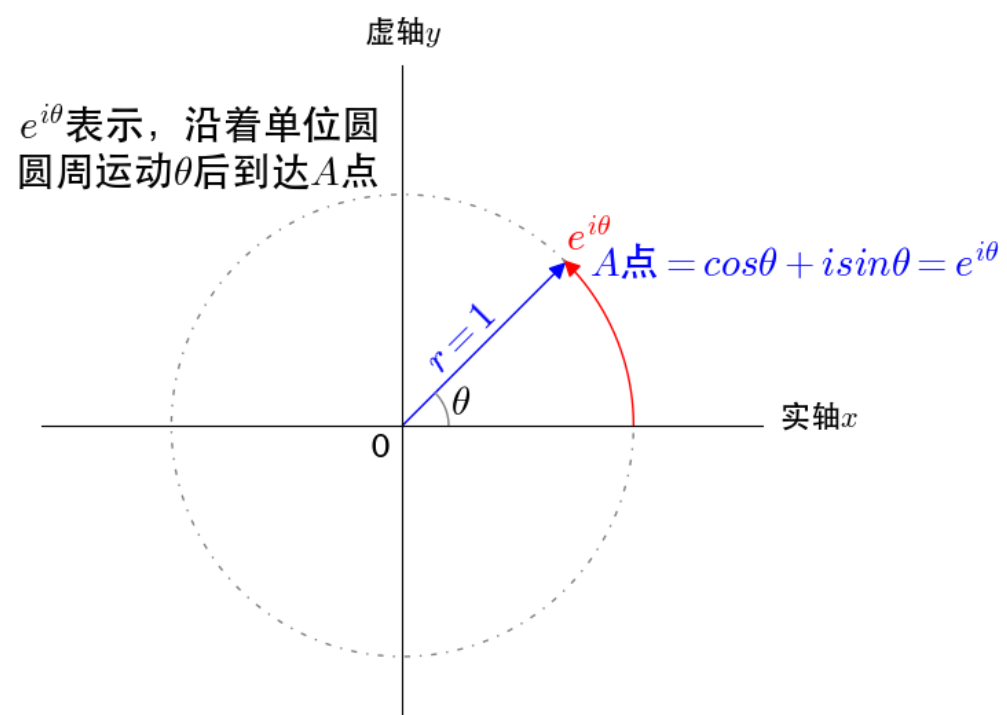
0 Eular Equation

\(\begin{aligned} e^{i\theta}&=\cos\theta+i\sin\theta \\ e^{-i\theta}&=\cos\theta-i\sin\theta \\ \cos\theta&=\frac{e^{i\theta}+e^{-i\theta}}{2} \\ \sin\theta&=\frac{ie^{-i\theta}-ie^{i\theta}}{2} \end{aligned}\)

从几何角度看，

1 奇异矩阵和非奇异矩阵

奇异矩阵 Singular Matrix 非奇异矩阵 Non-singular matrix

从命名的角度来看 ‘Singular’ 意为 ‘单一的、非常的’。实际上也确实如此，因为相较于非奇异矩阵而言，奇异矩阵是非常稀少的

从几何的角度理解

1. 对于 $(1\times 1)$ 的矩阵，只有 $(0)$ 是奇异的
2. 对于 $(2\times 2)$ 的矩阵，可以将矩阵的两列理解为平面中的两条线段，只有在它们共线的时候矩阵才是奇异的，例如 \(\begin{pmatrix} 1 & 2 \\ 3 & 6 \end{pmatrix}\)
3. 对于 $(n\times n)$ 的矩阵，同理

从概念的角度来看 奇异矩阵的就是行列式等于 0 的方阵，可以从线性变换的方面来理解（详见 2.3.1）

2 行列式

【参考资料】 1.马同学：行列式的本质是什么？

行列式的本质是线性变换的伸缩因子

2.1 线性变换的几何直观

线性变换的几何直观有三个要点：

1. 变换前是直线的，变换后依然是直线
2. 直线比例保持不变（即在原线段上的两个三等分点在变换后依旧是新线段的三等分点）
3. 变换前是原点的，变换后依然是原点

   2.2 实现线性变换的矩阵

现有一向量 $A$，其原本的基向量 为 $i,j$

对 $A$ 进行一个旋转变换，即 $A_{new}=T_rA$。其中，线性变换矩阵 $T_r=[i’,j’]$ 将 $A$ 的基向量变换成 $A_{new}$ 的基向量，即将 $i,j$ 转变为 $i’,j’$

例如对于 \(T_r=\begin{bmatrix} \cos(\theta) & -\sin(\theta) \\ \sin(\theta) & \cos(\theta) \end{bmatrix}\)，下图显示了变换后的 $A_{new}$ 及其基向量

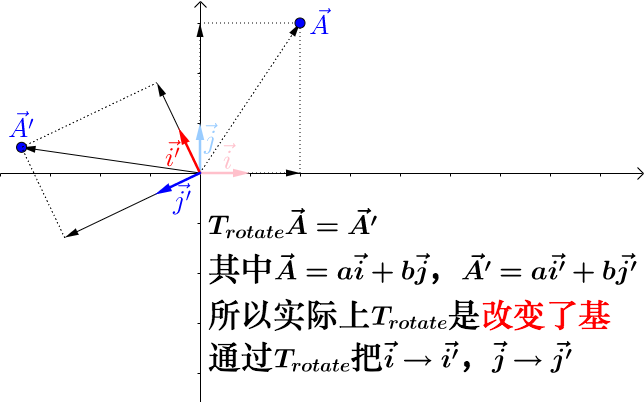
结论：对于线性变换矩阵 $T$，其列向量就是变换后的基向量，即 $T_r=[i’,j’]$，这就是矩阵真正的含义

2.3 行列式

结论：行列式就是线性变换的伸缩因子

例如对于 2.2 中的线性变换矩阵 $T_r$ \(|T_r|=\cos(\theta)^2+\sin(\theta)^2=1\)

这意味着旋转变换不会改变原图形的面积大小

2.3.1 行列式的值

1. $\det(T) > 1$ 当行列式大于 1，显然对于原图形起到放大作用
2. $\det(T) = 1$ 当行列式等于 1，此时不改变原图形的面积
3. $0 < \det(T) < 1$ 当行列式处于 0 到 1 之间，显然对于原图形起到缩小作用
4. $\det(T) = 0$ 行列式为 0 的矩阵也被称为奇异矩阵（Singular Matrix），其重要性质是不存在对应的逆矩阵，这一性质可以从线性变换的角度来理解： 当行列式等于 0，原图形将会被压缩成一个点或者一条直线，例如 \(T=\begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix}\text{ or }T=\begin{bmatrix} 0 & 0 \\ 0 & 5 \end{bmatrix}\) 此时，可以理解为线性变换矩阵 $T$ 已经将原图形完全破坏（降维打击），从而使之无法复原（不可能通过线性变换将直线或者点变换成面），因此奇异矩阵是不可逆的
5. $\det(T)<0$ 当行列式小于 0，改变基向量的方向，如下图

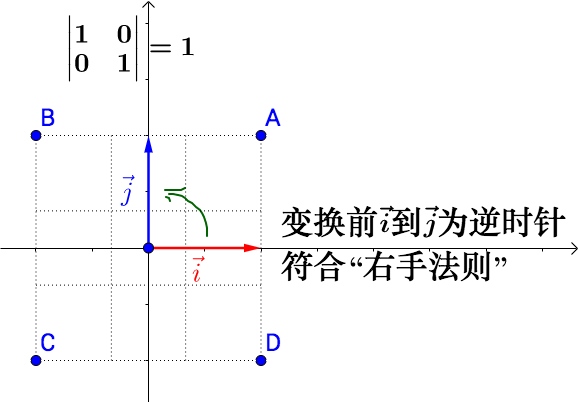
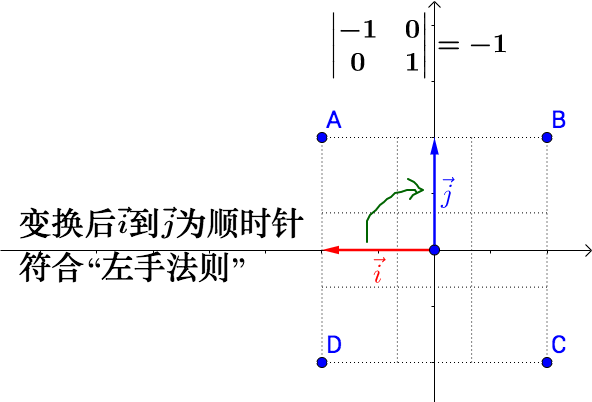
2.3.2 基于行列式来理解矩阵的性质

1. 矩阵乘法没有交换律 \(AB\neq BA\)

$AB$ 相当于用变换矩阵 $A$ 来变换矩阵 $B$ $BA$ 相当于用变换矩阵 $B$ 来变换矩阵 $A$ 这两者显然是不相等的

2. 二阶矩阵的行列式是列组成的平行四边形的面积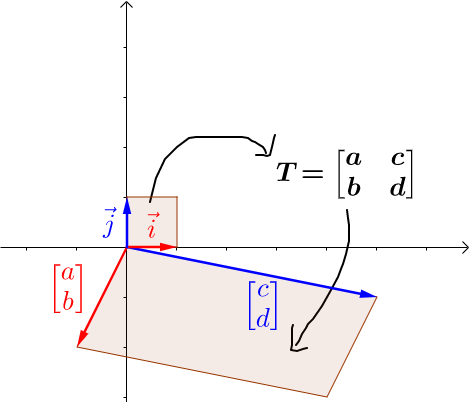

3 秩

Similar to Section 2，对于矩阵的秩，我们也可以从矩阵本身就代表着一个线性变换的角度来理解

1. 矩阵满秩意味着其所有列向量均线性无关 例如对于变换矩阵 $T_{n\times n}$，$T_{n\times n}$ 满秩则意味着该矩阵能将一个在 $\mathbb{C}^n$ 中的原图形变换成同样在 $\mathbb{C}^n$ 中的一个新图形

2. 矩阵不满秩即线性相关 例如对于变换矩阵 $T_{n\times n}$，若 $\text{rank}(T)=n-1$，则意味着该矩阵进行的是从 $\mathbb{C}^n$ 至 $\mathbb{C}^{n-1}$ 的线性变换 较极限的例子有 $\text{rank}(T)=0$（被压缩成点），$\text{rank}(T)=1$（被压缩成线）