Jupyter Notebook: Simple neural network with sklearn 展示了一个简单的神经网络示例: 使用 sklearn.neural_network.MLPRegressor() 作为神经网络，根据波士顿地区房子的房间个数来预测房子的售价

1. Logistic Regression as a Neural Network

Jupyter Notebook: Logistic Regression with a Neural Network 展示了一个极简”神经网络“（用来判断图片中是否包含猫）: 只使用一个神经元（使用逻辑回归构建）

为什么叫“逻辑回归”呢？其实是音译，本质上是因为在线性的预测结果上套了一层 logistic function (sigmoid)，从而让预测结果 $\in(0,1)$

1.1 Model

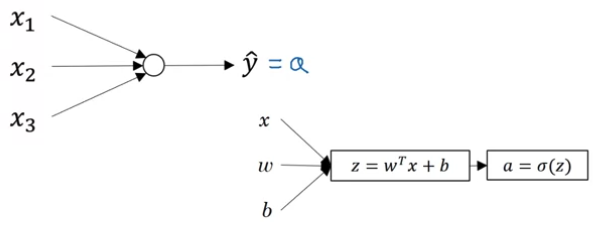
• Given $x\in\R^{n_x}$, want $\hat{y}=P(y=1\vert x)$
• Prameters: $\omega\in\R^{n_x},b\in\R$
• Output $\hat{y}=\sigma{(\omega^Tx+b)}$

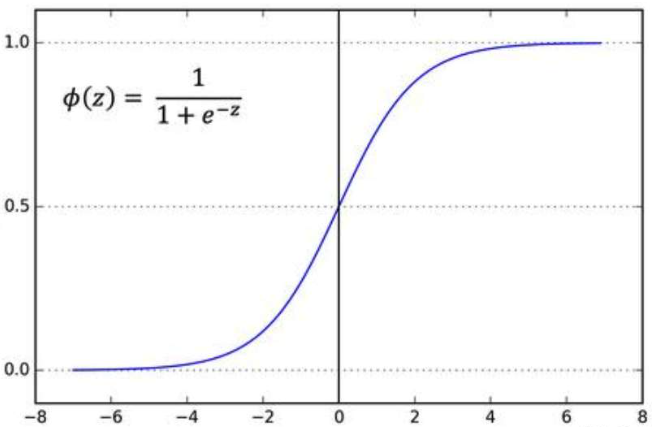
Sigmoid Function: $\sigma(z)=1/(1+e^{-z})$

1.2 Cost Function

Object: Given ${(x^{(1)},y^{(1)}),…,(x^{(m)},y^{(m)})}$, want $\hat{y}^{(i)}=\sigma(\omega^Tx^{(i)}+b)\approx y^{(i)}$

• Loss function: \(\mathcal{L}(\hat y,y)=-(y\log\hat{y}+(1-y)\log(1-\hat{y}))\)
• Cost function: \(J(\omega,b)=\frac{1}{m}\sum_{i=1}^m\mathcal{L}(\hat{y}^{(i)},y^{(i)})\)

1.3 Gradient Descent

Object: optimize $w,b$ to minimize $J(w,b)$

Process: repeat ($\alpha$ is the learning rate, usually from 0.0001 to 0.01)

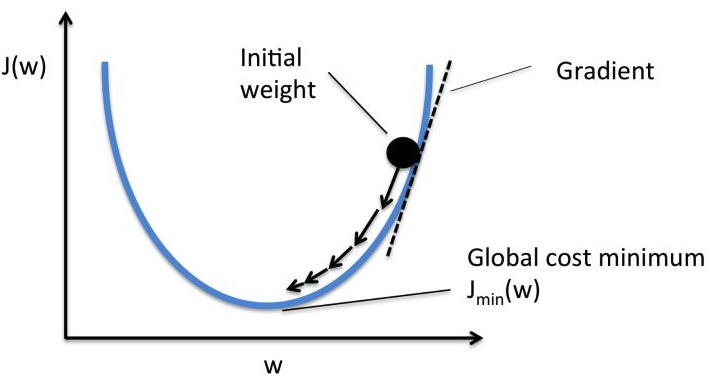
1.4 Calculate Derivatives & Vectorization

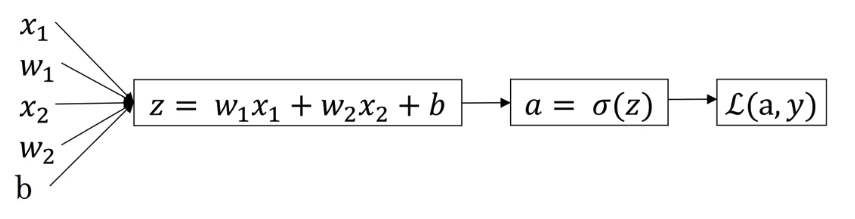
Vectorization:

In Python

for iter in range(1000):
    Z = np.dot(w.T,X) + b
    A = Sigmoid(Z)
    dZ = A - Y
    dw = np.dot(X,dZ.T)/m
    db = np.sum(dZ)/m
    
    w = w - alpha*dw
    b = b - alpha*db

2. Neural Network

上一节介绍了单个 Logistic Regression 神经元，而神经网络则是由多个这样的神经元组成的多重网状结构

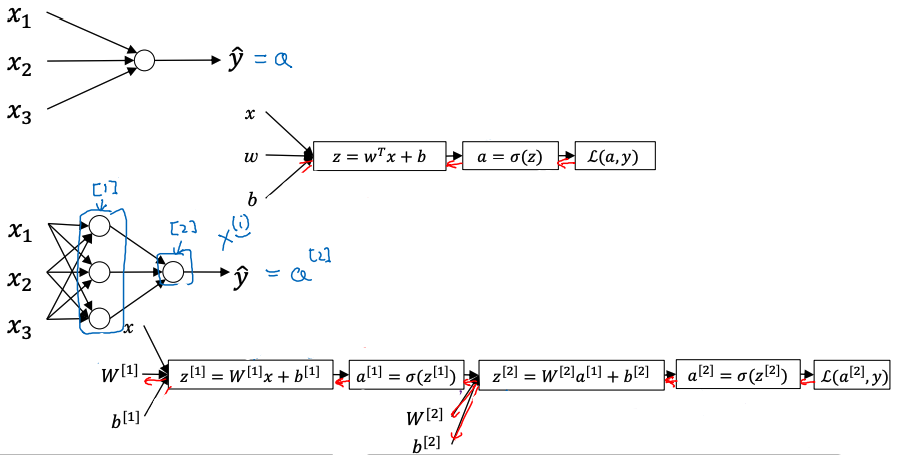
Representation

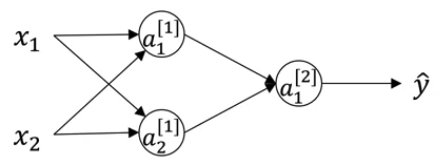
下图展示了一个 2 layer NN (1 hidden + 1 output)，使用右上角方框内的数字表示层数

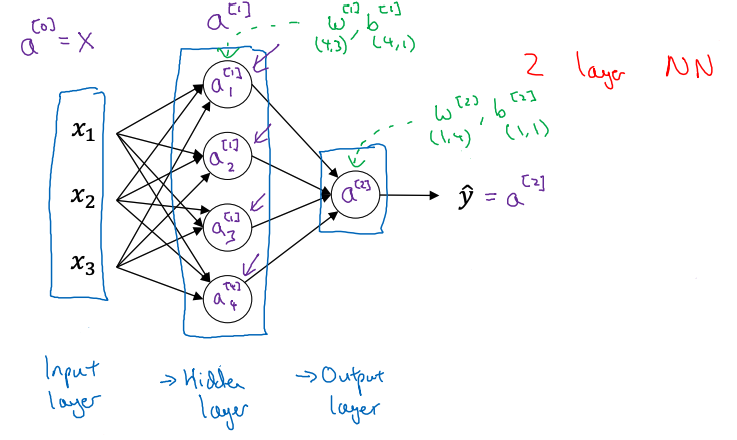
2.1 Forward Propagation

Vectorization with $m$ samples

2.2 Activation Functions

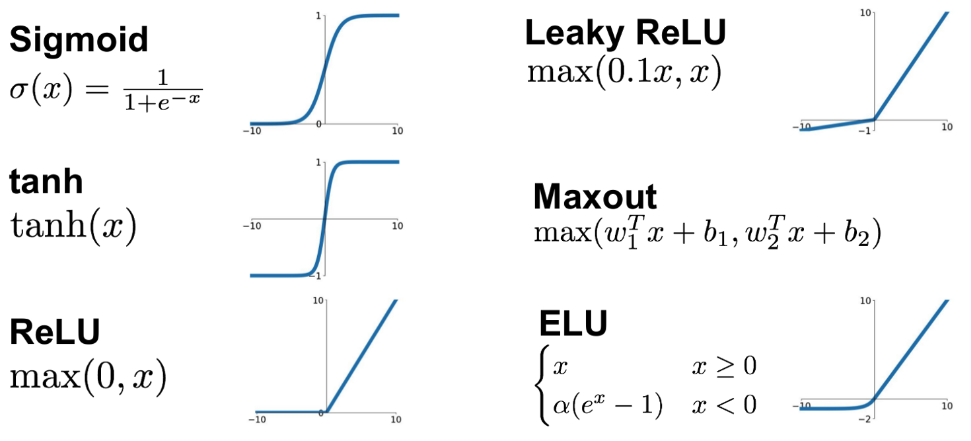
Sigmoid

一般只作为 Binary Classification 的 output layer’s activation funcction

tanh

Better than Sigmoid if want strong derivatives & big learning steps. 因为当 $x$ 的值在0附近时，tanh 的斜率要大于 Sigmoid

ReLU (Rectified Linear Unit)

Mostly used. 相较于 Sigmoid 和 tanh，ReLU 右侧的斜率始终为1，这避免了像 Sigmoid 那样当 $x$ 数值较大时因为斜率过低而导致学习速率过慢的情况

Why need NON-linear activation functions?

可以发现上述所有的激活函数都是非线性的，这是因为n层线性的激活函数等同于1层

Derivatives

对于 ReLU and Leaky ReLU, 它们的求导为常数

2.3 Backward Propagation (Gradient Descent)

例如对下图神经网络，假设 Hidden Layer 使用未知激活函数 $g(x)$，Output Layer 使用 $g(x)=\sigma(x)$ 作为激活函数

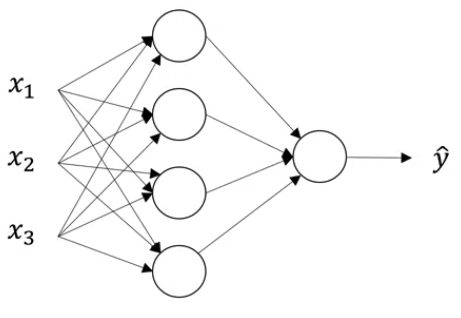
Layer Dimensions: 使用 $n^{[i]}$ 表示每个 Layer 中神经元（或是输入输出）的个数

• $n^{[0]}=n_x=3$
• $n^{[1]}=4$
• $n^{[2]}=1$

Output Layer(第二层): 因为使用 $g(x)=\sigma(x)$，直接参照 Chapter 1.4

Hidden Layer(第一层): 使用未知激活函数（下式第一行中间的小点表示点乘）

2.4 Random Initialization

一般会把 $W_{init}$ 设置为一个比较小的随机数，把 $b_{init}$ 设置为 0

W1 = np.random.rand((4,3) * 0.01)
b1 = np.zeros((4,1))

为什么不把 $W_{init}$ 也设置为 0?

例如对于上图，如果把 $W_init$ 也设置为 0，那么 Hidden Layer 中两个神经元的初始公式就会一样，这会导致在反向传播的过程中它们所进行的更新也是同步的，因此就变成了两个一样的神经元

3. Deep L-layer Neural Network

Jupyter Notebook: Build Deep Neural Network Step by Step 展示了构建深层神经网络的详细过程

Jupyter Notebook: Deep Neural Network (Application) 在具体图像分类问题上应用上一个 Notebook 中所定义的函数

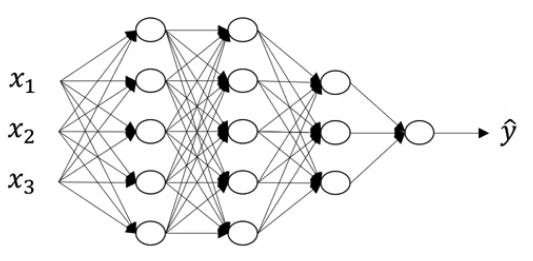
Notations

$L=4$ (#layers) $n^{[l]}=$ #units in layer $l$ ($n^{[0]}=n_x=3,n^{[1]}=n^{[2]}=5,…$) $a^{[l]}=g^{[l]}(z^{[l]})$ activations in layer $l$ $W^{[l]},b^{[l]}$ weights for $z^{[l]}$

2.1 Forward & Backward Propagation

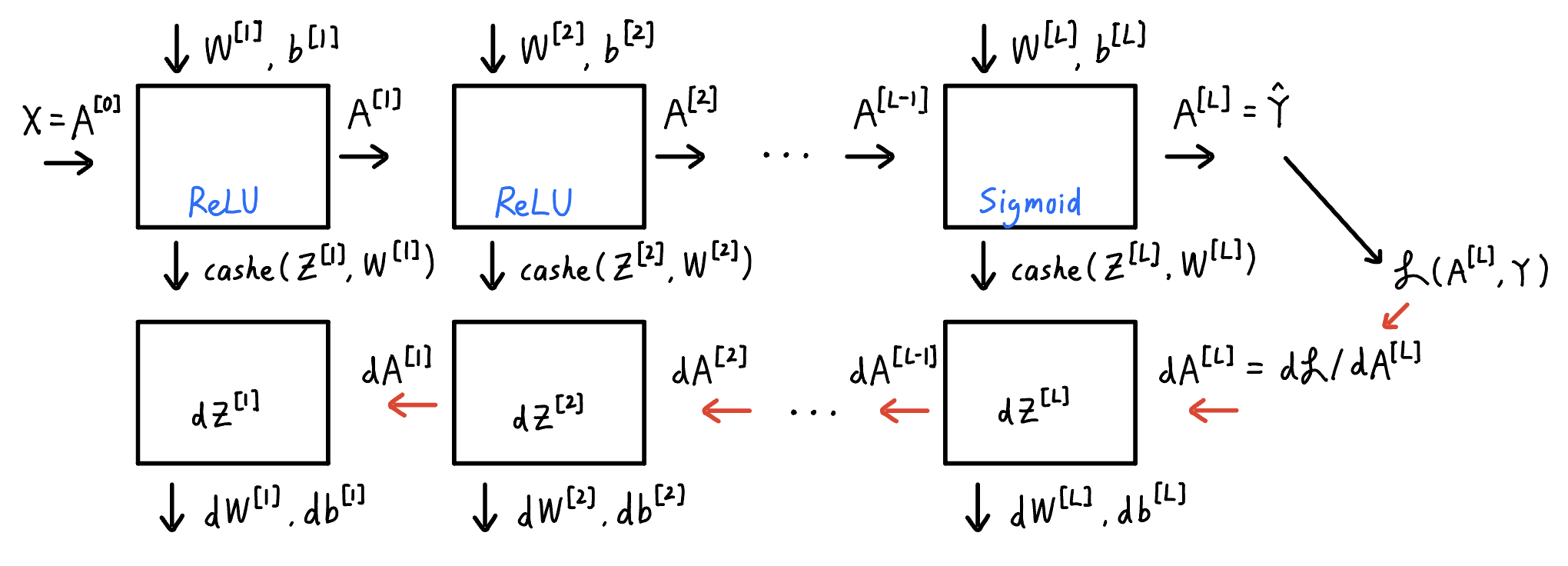
Forward Propagation Input $A^{[l-1]}$

Output $A^{[l]}$, cashe$(Z^{[l]},W^{[l]})$

where $A^{[0]}=X,A^{[L]}=\hat{Y}$

Backward Propagation

Input $dA^{[l]}$

Output $dA^{[l-1]},dW^{[l]},db^{[l]}$

2.2 Parameters vs. Hyperparameters

Parameters: $W^{[1]},b^{[1]},W^{[2]},b^{[2]}…$

Hyperparameters:

• learning rate $\alpha$
• #iterations
• #hidden layer $L$
• #hidden units of layer $l$
• choice of activation functions