1. PCA

1.1 Procedure

Given ${x^1,x^2,…,x^m}\in R^d$

(1) $\mu=\frac{1}{m}x^i$, $C=\frac{1}{m}\sum(x^i-\mu)(x^i-\mu)^T$

(2) Take eigenvectors

• take the eigenvector $w^1$ from $C$ corresponding to the largest eigenvector $\lambda^1$
• take $w^2$ from $C$ such that $w^2\perp w^1$ corresponding to the second largest $\lambda^2$

(3) Compute reduced represenation \(z^i=\begin{bmatrix} (w^1)^T(x^i-\mu)/\sqrt{\lambda^1}\\ (w^2)^T(x^i-\mu)/\sqrt{\lambda^2}\\ ... \end{bmatrix}\)

1.2 Limitation

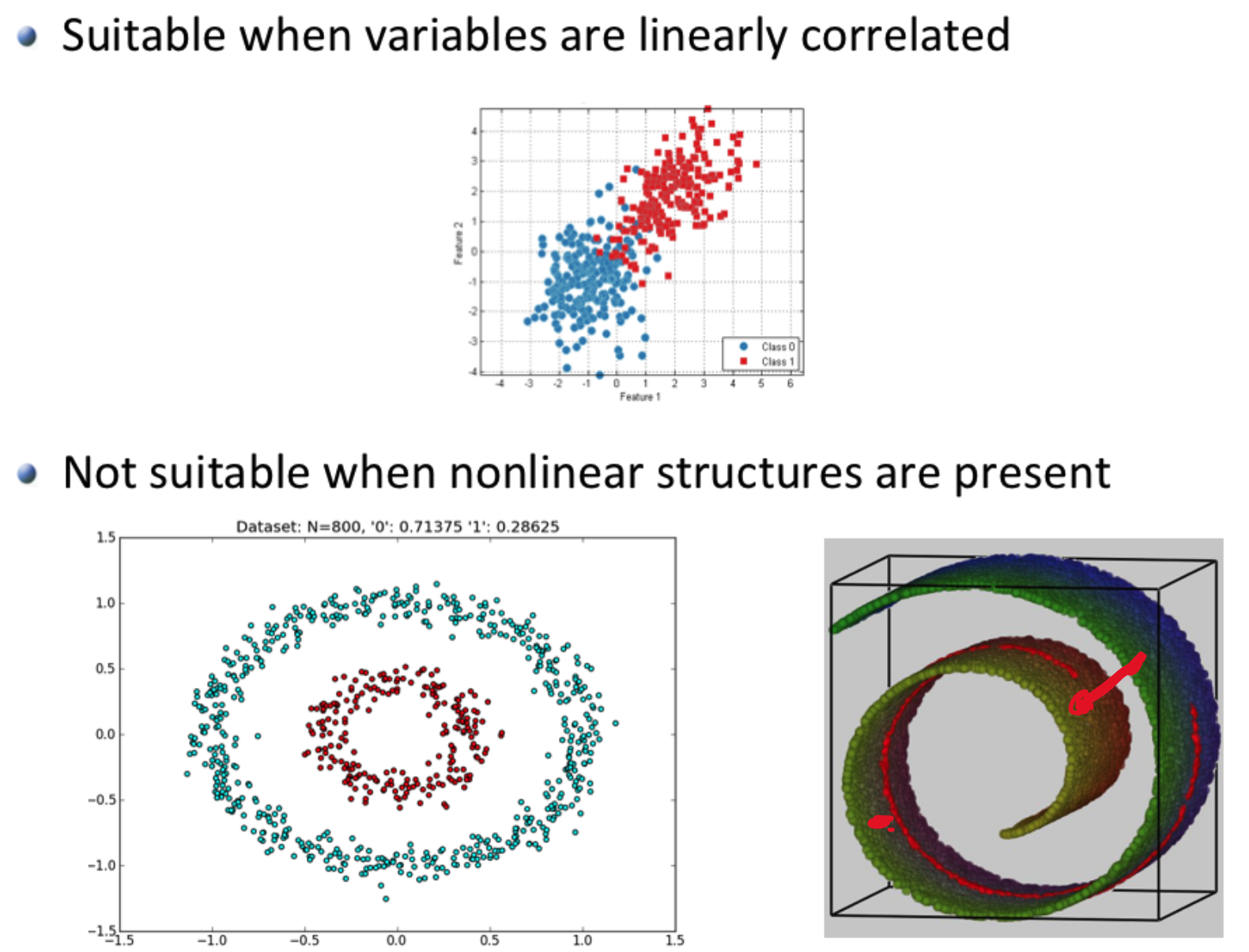
(use Isomap instead)

2. Isomap

Isomap is to use graph to solve the clustering problems like the two pictures above

2.1 Procedure

以下给出算法流程，具体解释详见 2.2

(1) Given $m$ data points, ${x^1,…,x^m}$

(2) Refer to Spectral Clustering, first define Adjacency Matrix $A\in R^{m\times m}$: \(A^{ij}=\begin{cases} \| x^i-x^j\| &\text{if } \| x^i-x^j\|\le\epsilon\\ 0 &\text{otherwise} \end{cases}\)

(3) Use a centering matrix $H=I-\frac{1}{m}\textbf{1}\textbf{1}^T$ to get \(C=-\frac{1}{2m}H^T(D^2)H\)

(4) Compute leading eigenvectors $w^1,w^2,…$ with largest eigenvalues $\lambda_1,\lambda_2,…$ of $C$ \(Z^T=[w^1,w^2,...]\begin{bmatrix} &\lambda_1^{-1/2} & & \\ & &\lambda_2^{-1/2}\\ & & &... \end{bmatrix}\)

2.2 Why Step(3) Above Make Sense?

Then construct Distance Matrix $D$ (could use Dijkstra), where \(D^{ij}=\text{graph distance from }i\text{ to }j\)

此时我们可以摒弃原数据，仅关注于 $D$。我们希望对 $D$ 进行主成分分析，回顾 PCA:

为了进行主成分分析，我们需要从 $D$ 中提取出 ${x^1,…,x^m}$，计作 $Z={z^1,…,z^m}$。由于 $D$ 是一个距离矩阵，我们很容易得出: \((D^{ij})^2=\|z^i-z^j\|^2\)

接下来的步骤就是为了一步步得出 $Z$:

1. $(D^{ij})^2={z^i}^Tz^i+{z^j}^Tz^j-2{z^i}^Tz^j$
2. 令 $a=[{z^1}^Tz^1,…,{z^m}^Tz^m]^T$, $\textbf{1}=[1,…,1]^T_{m\times 1}$, 则有 \(D^2=a\textbf{1}^T+\textbf{1}a^T-2Z^TZ\)
3. 构造矩阵 $H$ 用于标准化 $Z$: $H=I-\frac{1}{m}\textbf{1}\textbf{1}^T$
4. 标准化 $Z\to$ $\tilde{Z}=ZH=Z(I-\frac{1}{m}\textbf{1}\textbf{1}^T)=Z-\mu\textbf{1}^T$
5. 此时，我们终于可以构造用于 PCA 的协方差矩阵了: \(C=\frac{1}{m}\tilde{Z}^T\tilde{Z}=\frac{1}{m}H^TZ^TZH\)

6. 最后，因为难以计算出 $Z$，我们需要将 $Z^TZ$ 用 $D,H$ 替换: \(H^T(a\textbf{1}^T)H=H^T(\textbf{1}a^T)H=0\)

   \[C=-\frac{1}{2m}H^T(a\textbf{1}^T+a\textbf{1}^T-2Z^TZ)H\] \[\boxed{C=-\frac{1}{2m}H^T(D^2)H}\]