Parametric models Histogram Kernel density estimator Mixture of Gaussia
1. Models
1.1 Parametric Models
Models which can be described by a fixed number of parameters
- Discrete case: eg. Bernoulli distribution
- Continuous case: eg. Gaussian distribution
Estimation of parametric models A very popular estimator is the maximum likelihood estimator (MLE)
- Assume $m$ data points $D={x^1,…,x^m}$ are iid from some distribution
- Want to fit the data with a model $P(x\vert\theta)$ with parameter $\theta$ \(\theta=\argmax_{\theta}\log\prod_{i=1}^mP(x^i\vert\theta)\)
1.2 Non-parametric Models
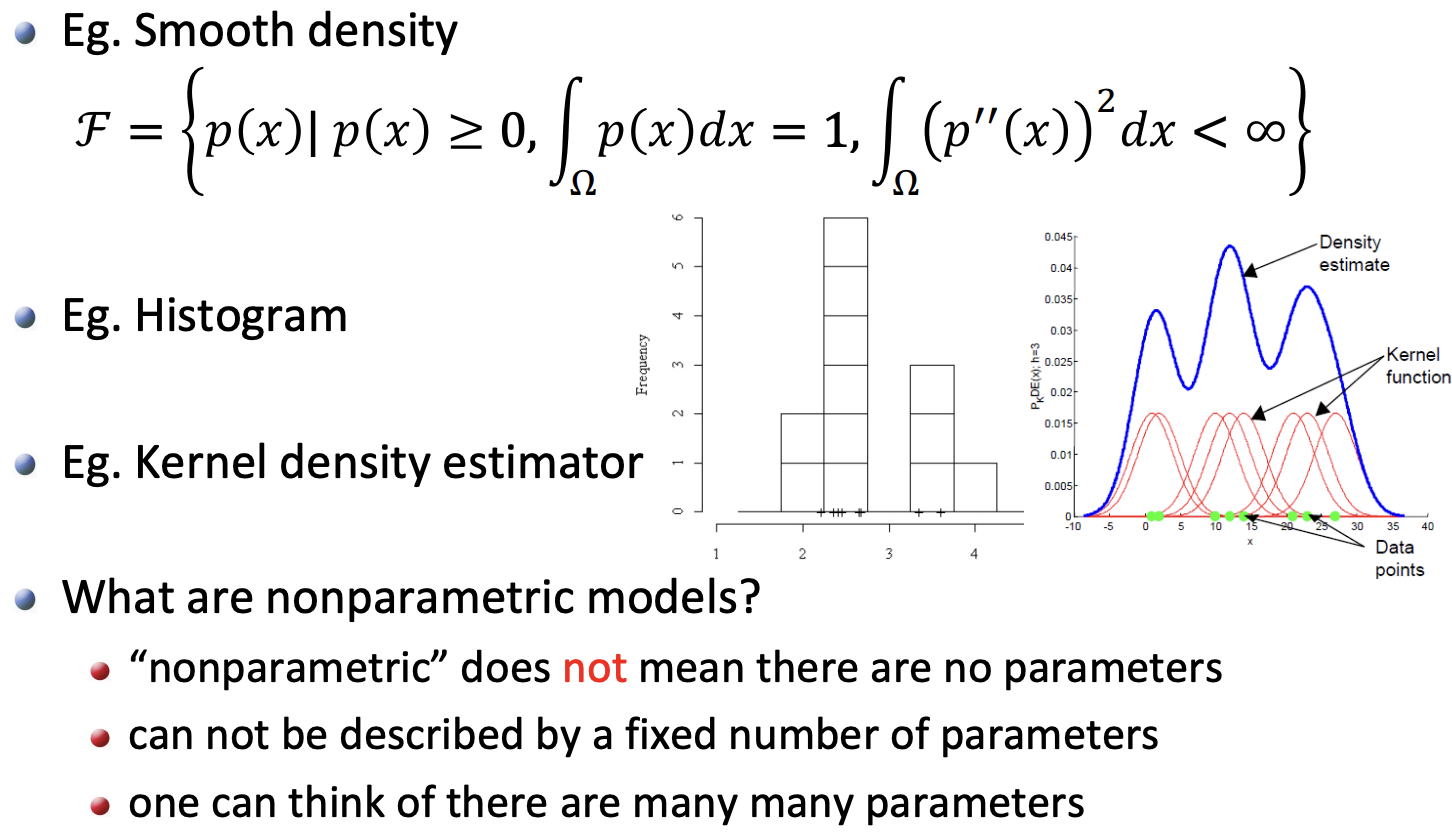
1.2.1 Gaussian mixture model
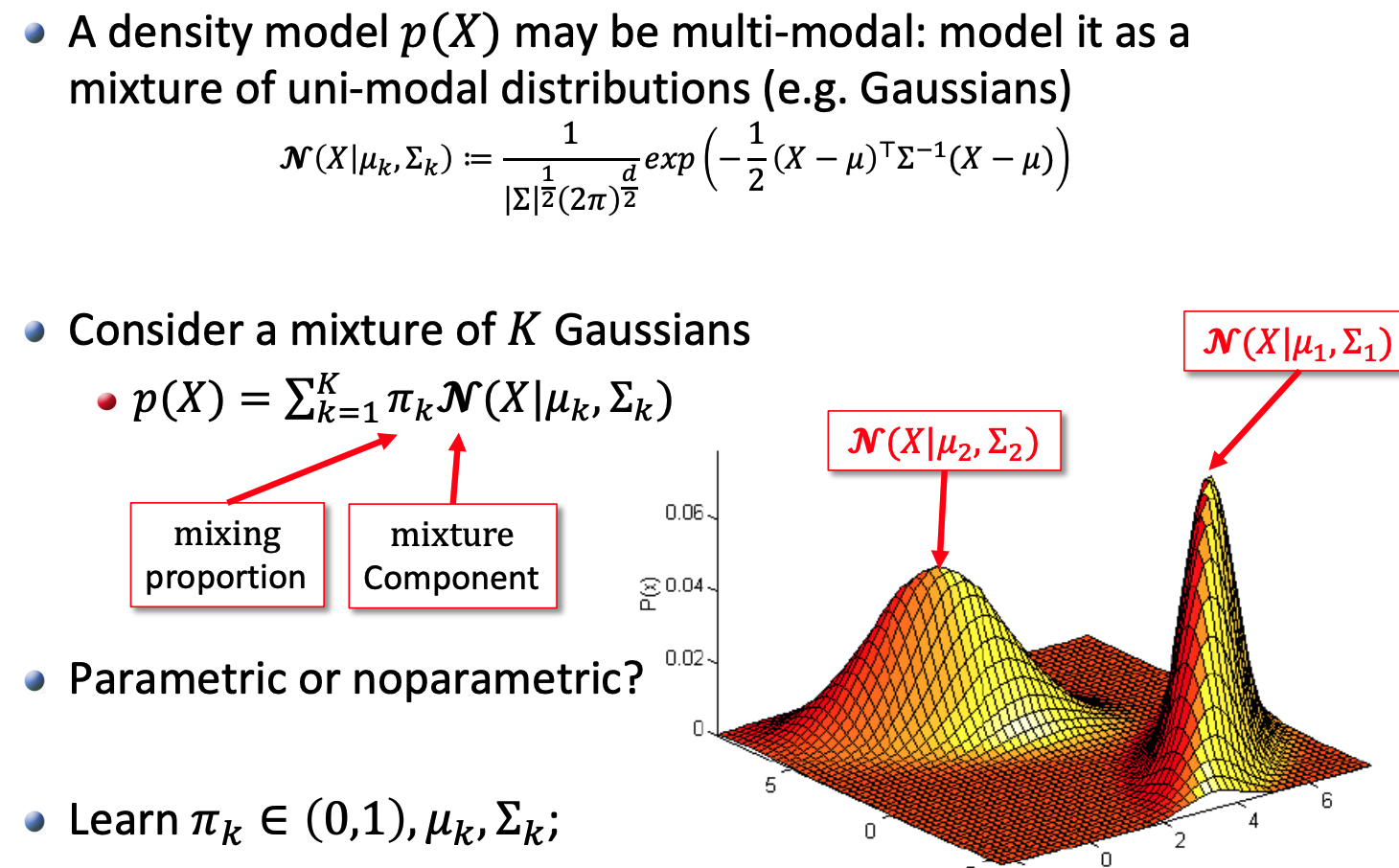
1.3 Parametric vs. Non-parametric
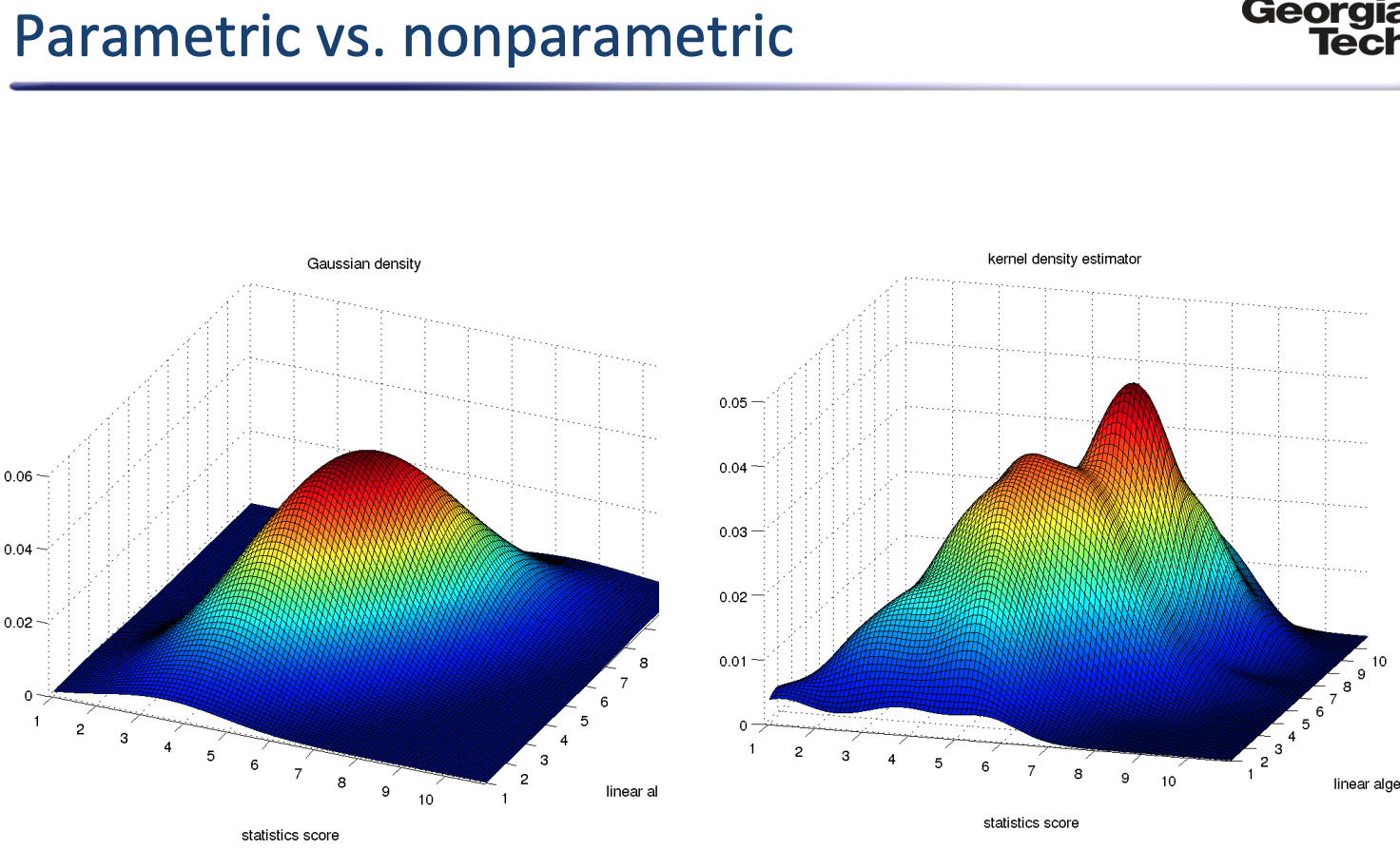

2. EM Algorithm
基于 Gaussian mixture model,我们怎么去算出参数 $\theta=(\pi_k,\mu_k,\Sigma_k)$ 呢?首先给出具体: 
where
- $\tau^i_k\in[0,1]$ 表示 data $i$ 属于 Gaussian component $k$ 的概率。在 E-step 中更新
- $\pi_k$ 表示 Gaussian component $k$ 在整个 Gaussian mixture 中的占比 $(\sum_{k=1}^K\pi_k=1)$
2.1 Why this?
上面的步骤看上去很合理,但是,为什么呢?这就涉及到 EM Algorithm 的核心思想: Expectation Maximization
Objective: 找出最合适的参数 $\theta^=(\pi_k^,\mu_k^,\Sigma_k^)$ 以最大化 $P(X\vert \theta)$
\[\theta^*=\argmax_\theta l(\theta;D)\]where
- $l(\theta;D)$ is the log-likelihood function \(\begin{aligned}l(\theta;D) &=\log\prod_{i=1}^mp(x^i)\\ &=\log\prod_{i=1}^m\sum_{z^i=1}^Kp(x^i, z^i)\\ &=\log\prod_{i=1}^m\sum_{z^i=1}^Kp(x^i\vert z^i)p(z^i)\\ &=\log\prod_{i=1}^m\sum_{z^i=1}^KN(x^i\vert \mu_{z^i},\Sigma_{z^i})\pi_{z^i}\\ \end{aligned}\)
- $z^i\in{1,2,…,K}$, $z^i=k$ 表示 data $i$ 属于 Gaussian component $k$
2.1.1 Hard to solve directly
此时观察我们的 $l(\theta;D)$,它是一个非常复杂的 nonconvex function,这意味着我们无法直接通过求导的方式求出 $\theta^*$
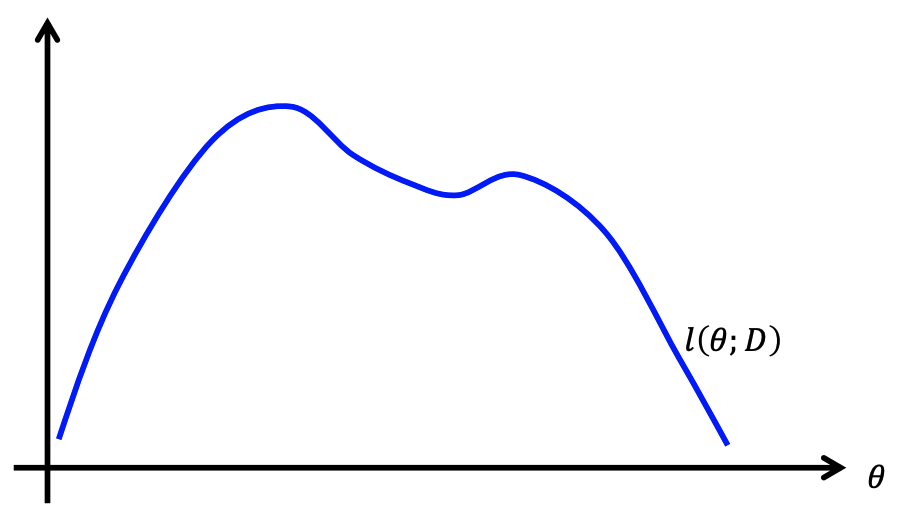
导致这种情况的根本原因在于 $l(\theta;D)$ 的公式中包含了对数函数内的函数加法 $\log(\sum…)$ \(\begin{aligned} l(\theta;D) &=\log\prod_{i=1}^m\sum_{z^i=1}^Kp(x^i, z^i)\\ &=\sum_{i=1}^m\log\sum_{z^i=1}^Kp(x^i, z^i) \end{aligned}\)
有没有一种方法能够把 $\log$ 函数放进两个求和里面呢? ($\sum\sum\log$)
2.1.2 Jensen Inequality
根据 Jensen 不等式,对于任何凹函数 $f(x)$,都有:
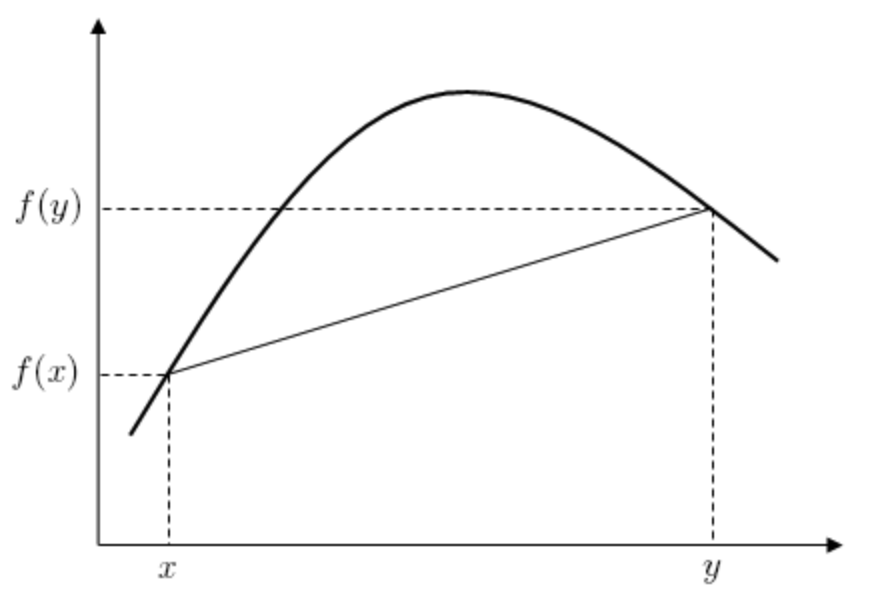
已知 $\log$ 函数是一个凹函数,那么为了使得 $l(\theta;D)$ 能够被计算,我们需要把 $\sum_{z^i=1}^Kp(x^i, z^i)$ 改造成一个对于 $z^i$ 的期望 (这是因为在对数函数内,$x^i$ 相当于定值,而 $z^i$ 为变量) \(\sum_{z^i=1}^Kp(x^i, z^i) =\sum_{z^i=1}^Kp(z^i\vert x^i)\frac{p(x^i, z^i)}{p(z^i\vert x^i)} =E_{p(z^i\vert x^i)}\Big[\frac{p(x^i, z^i)}{p(z^i\vert x^i)}\Big]\)
Therefore: \(l(\theta;D)=\sum_{i=1}^m\log\sum_{z^i=1}^Kp(x^i, z^i)\geq \sum_{i=1}^m\sum_{z^i=1}^Kp(z^i\vert x^i)\log\Big(\frac{p(x^i, z^i)}{p(z^i\vert x^i)}\Big)=f(\theta)\)
再提取出 $f(\theta)$ 中的常数部分 $c=\sum\sum p(z^i\vert x^i)\log p(z^i\vert x^i)$,可得 \(l(\theta;D)\ge f(\theta)=\sum_{i=1}^m\sum_{z^i=1}^Kp(z^i\vert x^i)\log(p(x^i,z^i))-c\)
因此,通过 Jensen 不等式,我们可以得到 $l(\theta;D)$ 的下界 $f(\theta)$
2.2 Expectation Step
这里以 Section 2 开头的 Gaussian Mixture Model 为例,可得:
- $p(z^i=k\vert x^i)=\tau_k^i$
- $p(x^i,z^i)=p(z^i)p(x^i\vert z^i)=\pi_{z^i}N(x^i\vert\mu_{z^i},\Sigma_{z^i})$
Expectation step 基于上一轮的观测数据 $(\pi_k,\mu_k,\Sigma_k)$,来计算各个 Gaussian components 对于各个数据点的后验分布: \(\tau_k^i=p(z^i\vert x)=\frac{p(x^i,z^i=k)}{p(x^i)}=\frac{\pi_kN(x^i\vert\mu_{k},\Sigma_{k})}{\sum_{k'=1}^K\pi_{k'}N(x^i\vert\mu_{k'},\Sigma_{k'})}\)
2.3 Maximization Step
Maximization Step 就是根据在 E-step 更新后的后验分布,更新参数 $\theta=(\pi_k,\mu_k,\Sigma_k)$。以更新 $\pi_k$ 为例:
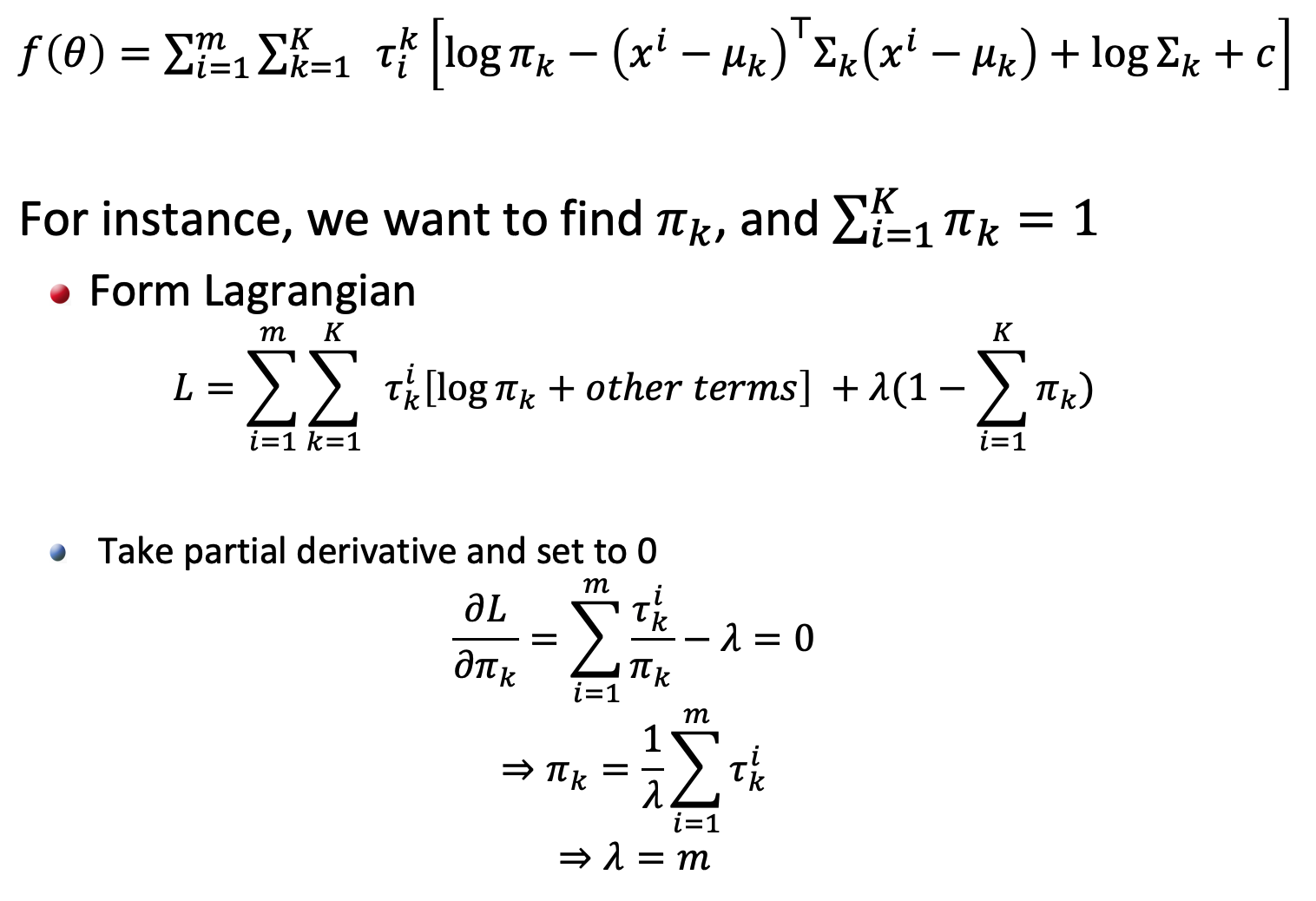
2.4 Conclusion
以上算法的核心思想在于:
- 构造目标函数的下界 (concave function) $f_1(\theta)$
- 使用 EM 算法来更新参数
- 根据新的参数构造新的下界 $f_2(\theta)$
- 不断重复 2,3 直到收敛
可以用下图概括:
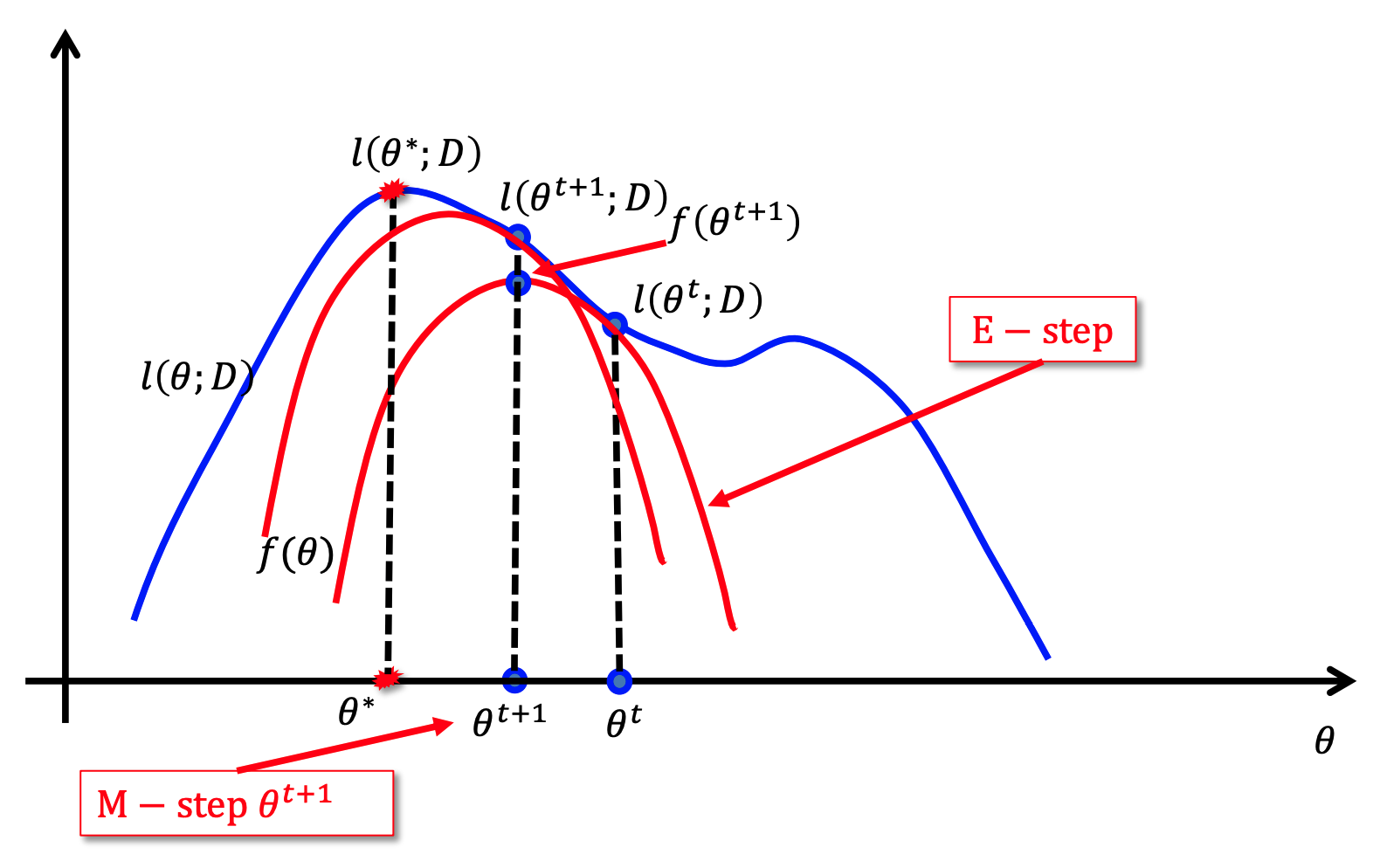
Document Information
- Author: Zeka Lee
- Link: https://zhekaili.github.io/0004/06/03/unsupervised-Density-Estimation/
- Copyright: 自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)