Advanced topics
- Generalization ability Overfitting Bias-variance trade-off Cross-validation
- Kernel methods Kernel functions Feature spaces Kernel tricks
- Graphical models Directed graphical models (HMM) Undirected applications (MRF)
- Reinforcement learning
1. Generalization
1.1 Bias-variance trade-off
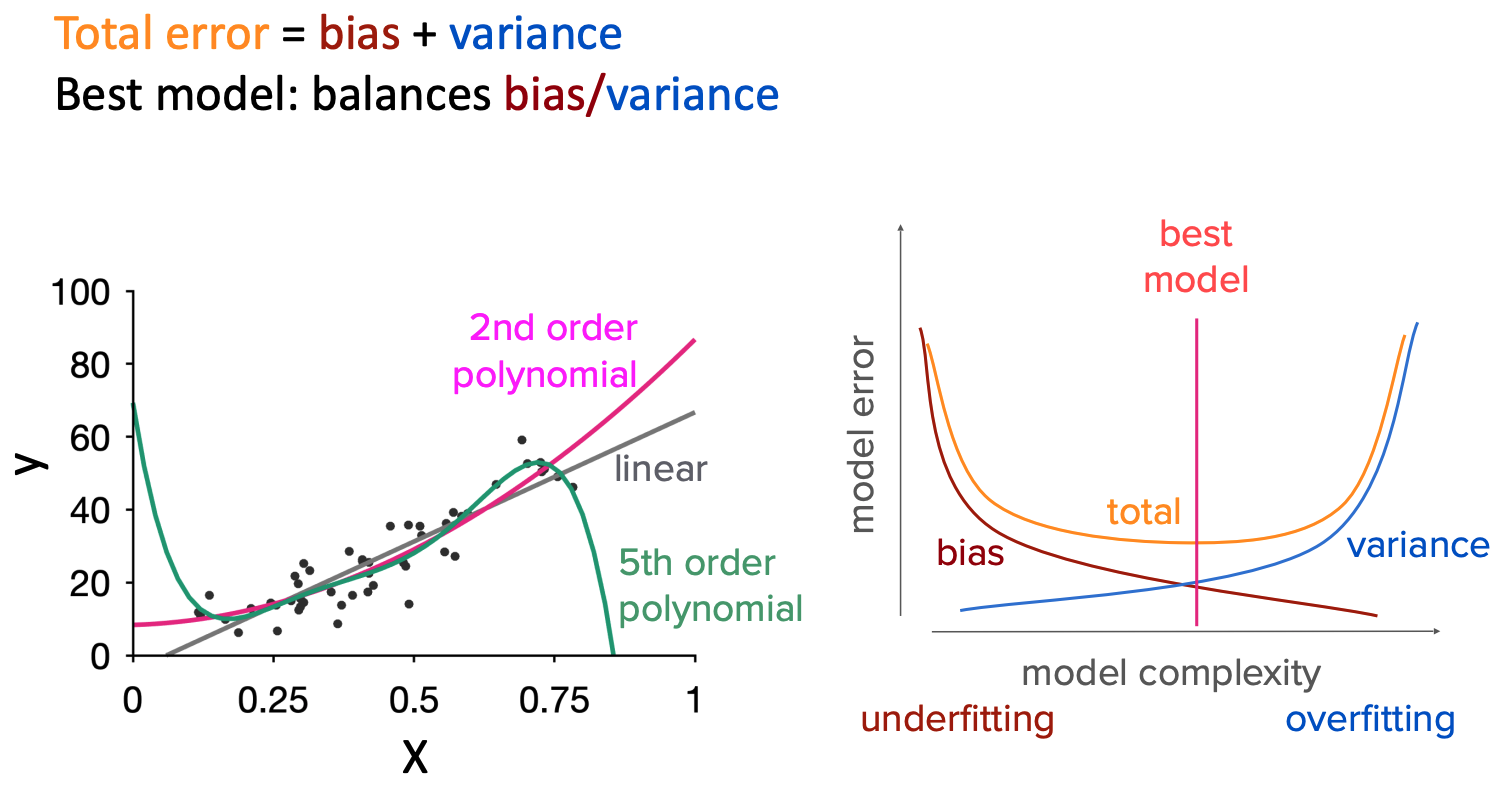
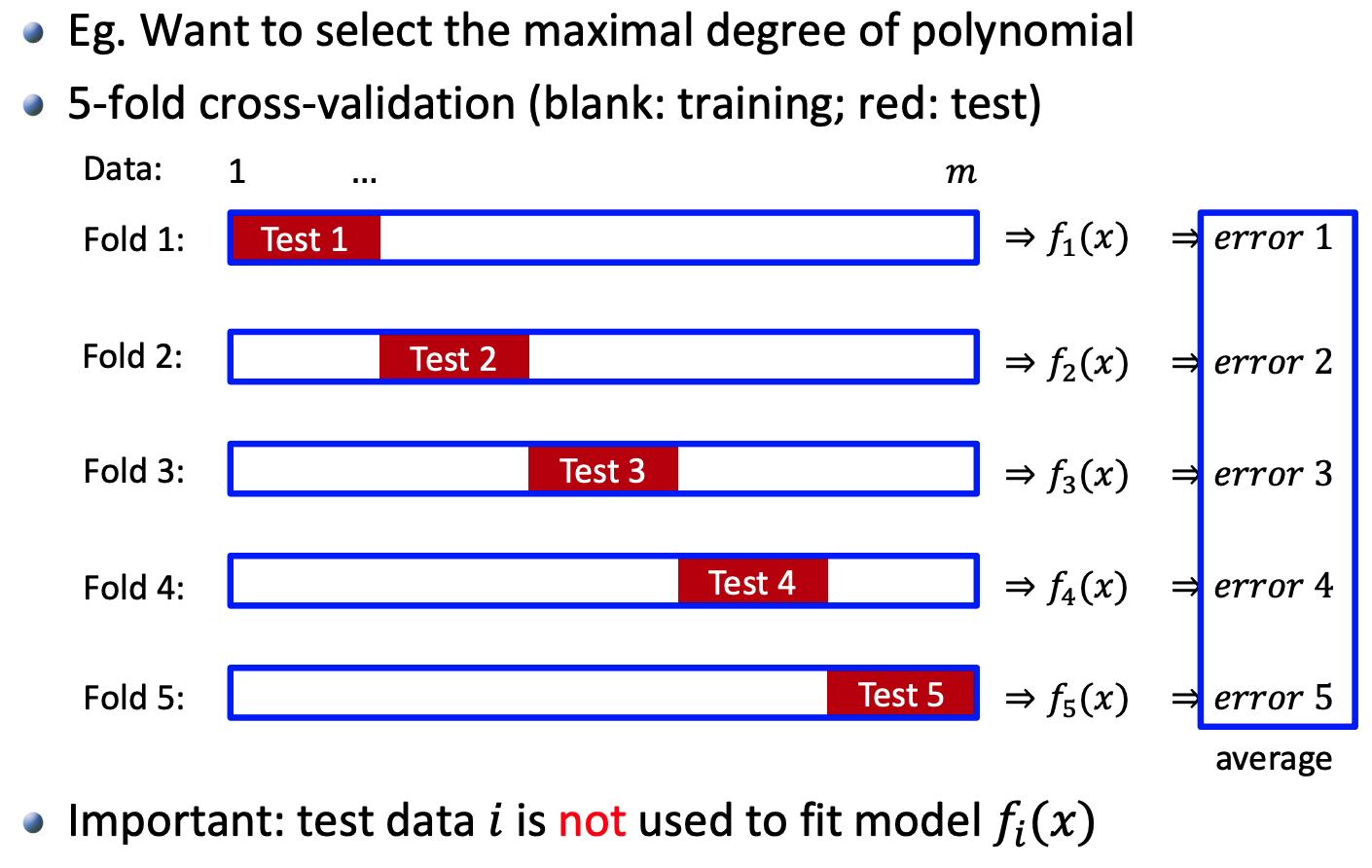
1.2 Cross-validation
2. Kernel
Kernels are implicit nonlinear feature mapping, rather than computing the features explicitly, and then compute inner product
For example: 
Typical kernels for vector data: 
3. Hidden Markov Model (HMM)
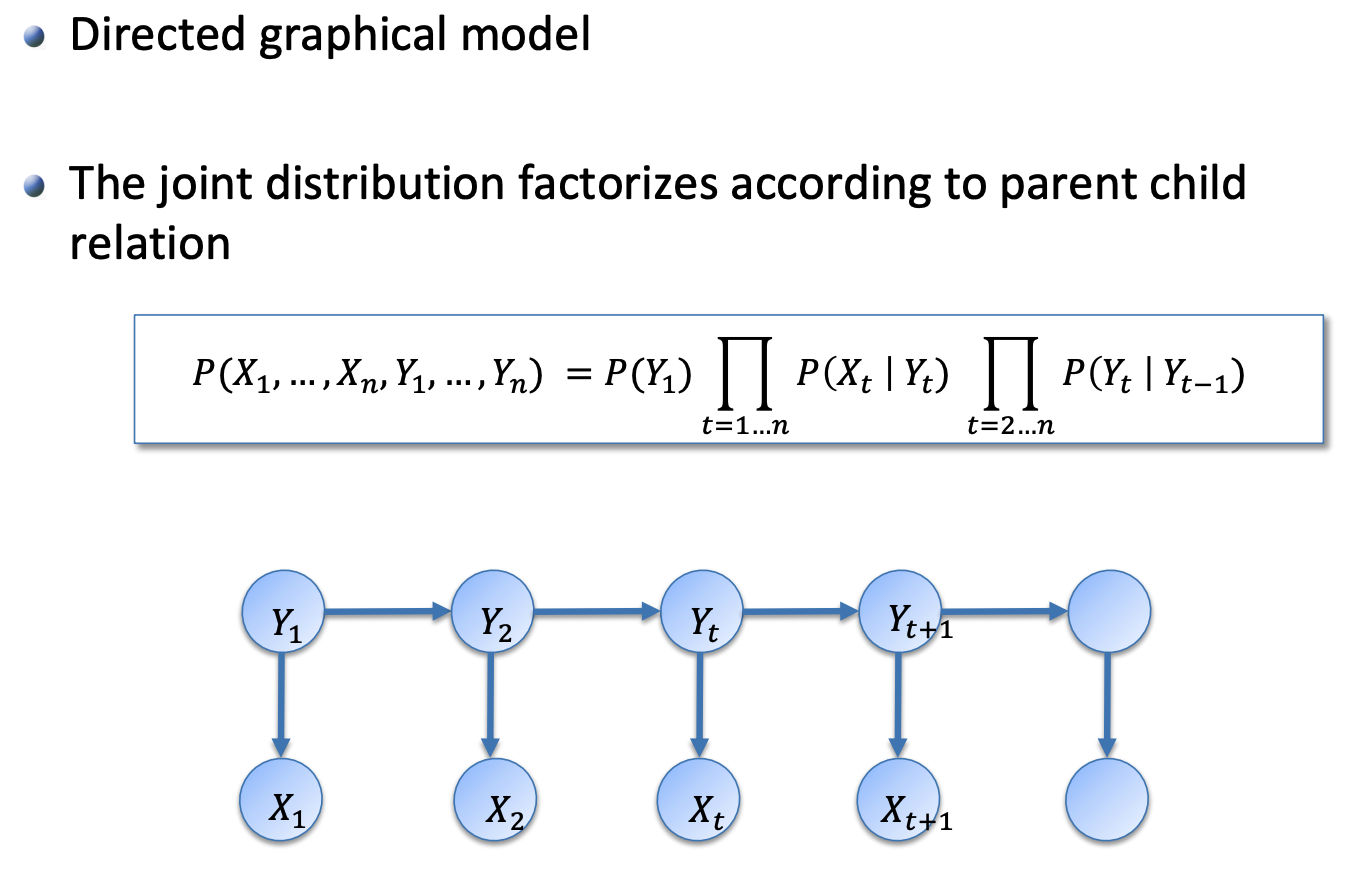
3.1 Generate HMM
We have 4 boxes with different number of red balls and white ball.
| Box Number | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| #Red Ball | 5 | 3 | 5 | 8 |
| #White Ball | 5 | 7 | 4 | 2 |
Now we want to pick $T$ balls from these 4 boxes using the following rules:
- First, we know the initial probability distribution of 4 boxes, denoted as $\pi=[\pi_i]^T_4$. For example, we could assume uniform distribution: \(\pi=[0.25\text{ }0.25\text{ }0.25\text{ }0.25]\)
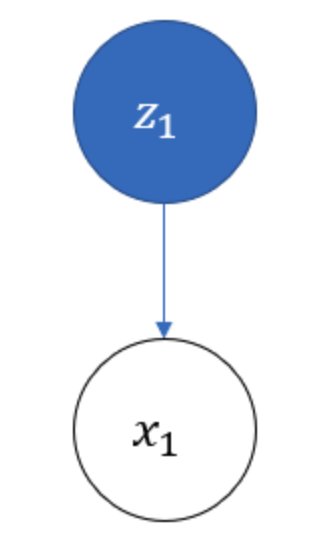
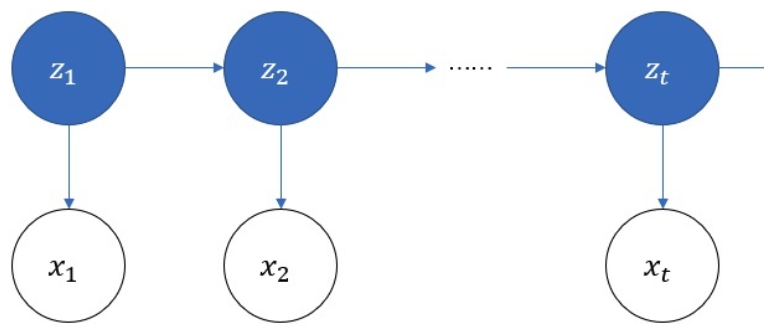
- Then, we choose the first box to pick ball, the first chosen box is denoted as $z_1$. There are 4 possible values of $z_1$, denoted as $q_i(i\in{1,2,3,4})$, representing 4 boxes
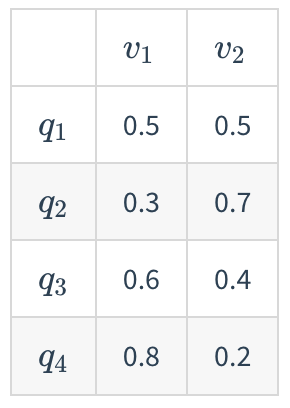
- In the first chosen box, we pick the first ball, denoted as $x_1$. There are 2 possible values of $x_1$, denoted as $v_j(j\in{1,2})$, representing red or white ball
- From the given table, we could get Observation Probability Matrix $B=[b_{ij}]{4\times 2}=[P(x=v_j\vert z=q_i)]{4\times 2}$:
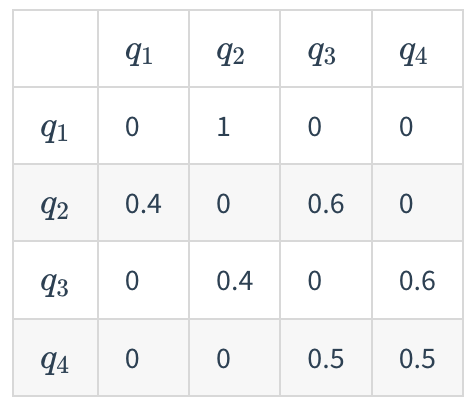
- After putting the fist ball back, we could choose the second box($z_2$) to pick ball, using the following rule:
- $P(z_{t+1}=q_2\vert z_t=q_1)=1$
- $P(z_{t+1}=q_1\vert z_t=q_2)=0.4$, $P(z_{t+1}=q_3\vert z_t=q_2)=0.6$
- $P(z_{t+1}=q_2\vert z_t=q_3)=0.4$, $P(z_{t+1}=q_4\vert z_t=q_3)=0.6$
- $P(z_{t+1}=q_3\vert z_t=q_4)=0.5$, $P(z_{t+1}=q_4\vert z_t=q_4)=0.5$
- Conclude the above rules into a Status Transition Matrix $A=[a_{ij}]{4\times 4}=[P(z{t+1}=q_j\vert z_t=q_i)]_{4\times 4}$
- Pick $x_2$ from $z_2$, and repeat
3.2 Calculate Probability
OBJ: Given $\lambda=(\pi,A,B)$ and observations $X=(x_1,…,x_T)$, calculate $P(X\vert\lambda)$
Becuase of hidden variable $Z$, to calculate $P(X\vert\lambda)$ directly: \(P(X\vert\lambda)=\sum_{Z}P(X,Z\vert\lambda)=\sum_{z_1}...\sum_{z_T}P(X,z\vert\lambda)\)
such calculation is too heavy $O(N^T)$. That’s why we need more effective algorithms:
3.2.1 Forward Algorithm
Define a Forward Probability $\alpha$ as the probablity of the status at time $t$ and the obvervations from time $1,2,…,t$ \(\alpha_t(i)=P(x_1,...,x_t,z_t=q_i\vert\lambda)\)
Its initial value is: \(\begin{aligned} \alpha_1(i)&=P(x_1,z_1=q_i\vert\lambda)\\ &=P(z_1=q_i\vert\lambda)P(x_1\vert z_1=q_i,\lambda)\\ &=\pi_ib_i(x_1) \end{aligned}\)
where $b_{i}(x_t)=b_i(x_t=v_j)=b_{ij}$
After calculating $\alpha_1(i)(i\in{1,2,3,4})$, we could than calculate $\alpha_2(j)$ \(\begin{aligned} \alpha_2(j)&=P(x_1,x_2,z_2=q_j\vert\lambda)\\ &=\sum_{i=1}^4P(x_1,x_2,z_1=q_i,z_2=q_j\vert\lambda)\\ &=\sum_{i=1}^4 \Big[P(x_2\vert x_1,z_1=q_i,z_2=q_j,\lambda)\Big]\Big[P(x_1,z_1=q_i,z_2=q_j\vert\lambda)\Big]\\ &=\sum_{i=1}^4\Big[P(x_2\vert z_2=q_j)\Big]\Big[P(z_2=q_j\vert x_1,z_1=q_i,\lambda)P(x_1,z_1=q_i\vert\lambda)\Big]\\ &=\sum_{i=1}^4\Big[P(x_2\vert z_2=q_j)\Big]\Big[P(z_2=q_j\vert z_1=q_i)P(x_1,z_1=q_i\vert\lambda)\Big]\\ &=\sum_{i=1}^4b_j(x_2)a_{ij}\alpha_1(i) \end{aligned}\)
therefore, for general case, we have \(\alpha_{t+1}(j)=\sum_{i=1}^Na_{ij}b_j(x_{t+1})\alpha_t(i)\)
3.2.2 Backward Algorithm
Define a Backward Probability $\beta_t(i)$ as the probablity of the obvervations from time $t+1,…,T$, given status $q_i$ at time $t$ \(\beta_t(i)=P(x_T,x_{T-1},...,x_{t+1}\vert z_t=q_i,\lambda)\)
Set the initial value $\beta_T(i)=1\text{ }\forall i$, because we cannot express it as a probability
… to be continued
3.3 Decoding

3.4 Learning

Document Information
- Author: Zeka Lee
- Link: https://zhekaili.github.io/0004/08/01/advanced-Kernel-and-HMM/
- Copyright: 自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)