References Coursera: Operations Research (1): Models and Applications (by National Taiwan University)

1. IP 中的选择问题

一个典型的选择问题： \(\max x_1+2x_2+3x_3+4x_4\)

1.1 选择变量 (item)

At least/most

• 至少在 item $1,2,3$ 中选择一个: $x_1+x_2+x_3\geq1$
• 至多在 item $1,3,4$ 中选择两个: $x_1+x_3+x_4\leq 2$

  A or B or A,B

• 选择 item $2$，否则需同时选择 item $3,4$ (可同时选): $2x_2+x_3+x_4\geq2$

  If-else

• 如果选择了 $2$，则需同时选择 $3$: $x_2\leq x_3$
• 如果选择了 $1$，则不能选择 $3,4$: $2(1-x_1)\geq x_3+x_4$

1.2 选择约束 (constraint)

LINKs Back: Current Note: #4 Ex: Scheduling

C1 or C2 满足约束1 or 约束2：$g_1(x)\leq b_1\text{ or }g_2(x)\leq b_2$

• 定义一个变量 $z\in{0,1}$ \(z=\begin{cases} 0 & \text{if }g_1(x)\leq b_1\text{ is satisfied}\\ 1 & \text{if }g_2(x)\leq b_2\text{ is satisfied} \end{cases}\)
• 利用变量 $z$ 定义约束, where $M_i$ is the upper bound of each LHS \(\begin{aligned} g_1(x)-b_1 & \leq M_1z\\ g_1(x)-b_1 & \leq M_2(1-z) \end{aligned}\)

At least/most 至少满足三个约束中的两个 $g_i(x)\leq b_i\;\;\; i=1,2,3$

• 定义三个变量 $z_i\in{0,1}$ \(z_i=\begin{cases} 1 & \text{if }g_i(x)\leq b_i\text{ is satisfied}\\ 0 & \text{if }g_i(x)\leq b_i\text{ is unsatisfied} \end{cases}\)
• 利用变量 $z_i$ 定义约束, where $M_i$ is the upper bound of each LHS \(\begin{aligned} g_i(x)-b_i & \leq M_i(1-z_i)\\ z_1+z_2+z_3 & \geq 2 \end{aligned}\)

2. Fixed-Charge Constraints

常见于生产问题，$S_i$ 为工厂 $i$ 的固定生产花费，$C_i$ 为每个生产的花费 \(\min \sum_{i=1}^nC_ix_i + \sum_{i=1}^nS_iy_i\)

where, \(\begin{aligned} x_i &= \text{production quantity at factory }i\\ y_i &= \begin{cases} 1 & \text{if factory }i\text{ produces some products}\\ 0 & \text{if produces nothing} \end{cases} \end{aligned}\)

3. Ex: Supply vs. Demand

选择最优的工厂建设地点，用于满足销售点的进货需求

定义变量:

销售地点 $i\in I$

• $y_i=1$ 表示销售点 $i$ 的进货需求被满足，反之为零
• $y_{ij}=1$ 表示销售点 $i$ 的进货需求被在 $j$ 地建设的工厂满足
• $h_i>0$ 表示销售点 $i$ 的进货需求量

工厂建设地点 $j\in J$

• $x_j=1$ 表示在地点 $j$ 建设工厂，反之为零
• $f_j>0$ 表示在地点 $j$ 建设工厂的固定费用
• $K_j>0$ 表示在地点 $j$ 建设的工厂的最大产能 根据是否需要使用 $K_j$，区分出两类问题 (un)capacitated facility location problem (CFL, UFL)

销售点与工厂之间的距离 $d_{ij}$

• $a_{ij}=1\text{ if }d_{ij}<s$ 表示在 $j$ 地建设的工厂能满足销售点 $i$ 的货物需求，反之为零

从工厂到销售点的单位运费 $c_{ij}$ (可以等于或正比于 $d_{ij}$)

3.0 问题分类

When to use ...?

• Set covering: required to take care of everyone e.g. 建设消防站
• Maximum covering: when budgets are limited
• Fixed charge location: when service costs depend on distance e.g. 建设物流中心

3.1 Set covering

目标: 在满足所有销售点进货需求的同时，最小化工厂建设数量 \(\min \sum_{j\in J}x_i\)

3.2 Maximum covering

目标: 在工厂建设数量不能超过 $p$ 个的同时，最大化满足销售点的进货需求 \(\max \sum_{i\in I}y_i\)

3.3 Fixed charge location

目标: 在满足所有销售点进货需求量的同时，最小化总的运输和建设费用 \(\min \sum_{j\in J}(f_jx_j+\sum_{i\in I}c_{ij}h_{i}y_{ij})\)

4. Ex: Scheduling

规划任务执行的顺序，以达成最优化目标

4.1 Completion time minimization (single machine)

定义变量:

• Job $j\in J$ has processing time $p_j$
• Completion time of job $j$ is $x_j$

下图假设当 jobs $1,2,…$ 按顺序依次执行时，则有 $x_n=\sum_{j=1}^np_j$

而实际上，job $i$ 亦可先于亦可后于 job $j$ 执行，即意味着必须只满足下式其一： \(x_j\geq x_i+p_j\text{ or }x_i\geq x_j+p_i\)

因此使用 Section 1.2 中介绍的方法，引入变量 $z_{ij}=1$ 表示 job $j$ 先于 job $i$ 执行： \(\begin{cases} x_i + p_j - x_j\leq M_1z_{ij}\\ x_j + p_i - x_i\leq M_2(1-z_{ij}) \end{cases}\)

其中，$M_1,M_2$ 必须满足“足够大”:

• 例如假设 $z_{ij}=1$，此时起作用的应该是第二个公式
• 因此第一个公式应该无效化，即 $M_1>\max(x_i+p_j-x_j)$

目标: 最小化所有任务的完成时间总和 \(\min \sum_{i\in J} x_j\)

4.2 Makespan minimization (parallel machines)

定义变量:

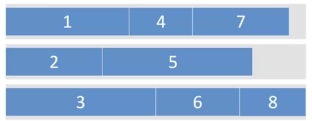
• Schedue $n$ jobs on $m$ parallel machines
• Job $j\in J$ has processing time $p_j$
• 定义变量 $x_{ij}=1$ 表示 job $j$ 由 machine $i$ 完成 因此，completion time of machine $i=\sum_{j\in J}p_jx_{ij}$
• Makespan $w$ is the max completion time \(w\geq \sum_{j\in J}p_jx_{ij}\;\;\;\forall i\in I\)

下图中的 makespan 等于最后一个机器的运行时间

目标: 最小化 makespan \(\min w\)

5. Ex: Vehicle Routing

以 Traveling salesperson problem 为例

目标：规划一条最短路径，从黄色结点出发，经过所有其他结点并最终返回黄色结点

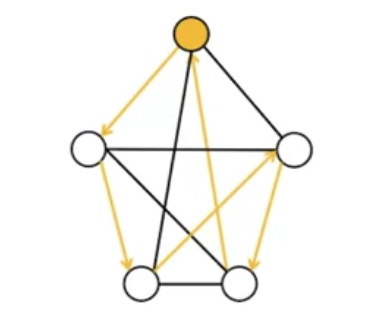
定义变量：

• 定义一个有向图表示路线网络 $G(V,E)$，所有结点之间均有一条边链接，因此共有 $n$ 个结点，$n(n-1)$ 条边
• $x_{ij}=1,(i,j)\in E$ 表示有向边 $(i,j)$ 被规划为路径中的一条边

约束条件：

• 结点总数为 $n$，因此最短路径也由 $n$ 条边组成
• 每个节点都有且仅有一条 incoming edge，一条 outgoing edge

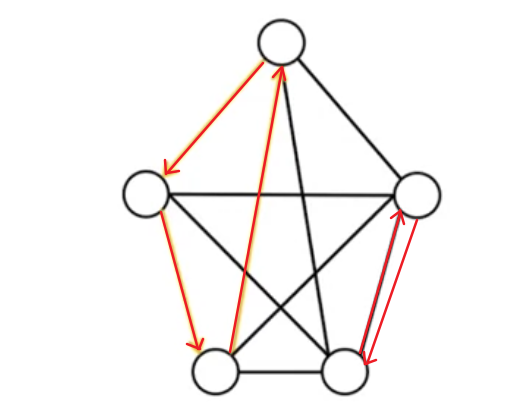
然而，仅有以上约束条件依旧是不够的，我们还需要消除路径规划中可能出现的 subtour 现象（如下图）

5.1 Eliminate subtours: method 1

对于任意一个至少包含两个结点的结点子集 $S\subsetneqq V, |S|\geq 2$，至多只能包含 $\vert S\vert-1$ 条被规划的边，从而避免 subtour \(\sum_{i\in S, j\in S, i\neq j}x_{ij}\leq \vert S\vert -1\)

总共有 $2^n$ 个结点子集，其中有 $n$ 个子集仅包含单个结点，一个子集不包含结点，一个子集包含 $n$ 个结点。因此共需要 $2^n-n-2$ 个这样的约束（因此该方法的局限在于，当 $n$ 较大时需添加的约束数量过大)

5.2 Eliminate subtours: method 2

引入变量 $u_i$ 表示结点的访问顺序，$u_i=m$ 表示 $V_i$ 是第 $m$ 个被访问到的结点。构建约束： \(\begin{aligned} & u_1 = 1\\ & 2\leq u_i\leq n\\ & u_i-u_j+1\leq(n-1)(1-x_{ij})\;\;\; i,j\neq 1 \end{aligned}\)

对于第三个约束

• 当 $x_{ij}=0$ 时，无事发生，因为 $u_i-u_j\leq n-2$ 一定成立
• 当 $x_{ij}=1$ 时，$u_i-u_j\leq -1$ 能够保证结点 $V_i$ 的访问顺序先于 $V_j$，从而避免出现如下图中 $x_{53}=1$ 的情况

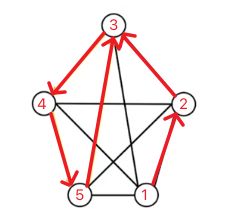
至于为什么不需要考虑 $i=1$ 或 $j=1$ 的情况呢？ 例如有四个节点1-4，上述条件能保证 $2\to3\to4$ 这条链的构成，那么对于节点1而言，有且只有两种情况 $4\to1\to2$ 或 $2\to1\to4$。第二种情况的方向看上去是错的，但其实因为此时环已经形成了，所以没有必要考虑方向性的问题，也就是说这两种情况是一样的且正确的

相比于方法一，方法二只需要添加 $n+(n-1)(n-2)$ 个约束

6. 使用 Excel 求解 IP

6.1 Ex: Personal scheduling

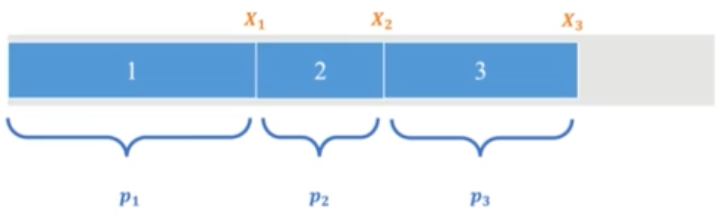
目标: 在满足工厂每日的在岗工人数量的需求下，最小化总的员工数量 |日期|在岗人数（人）| |-|-| |周一| 110| |周二| 80| |…|…| |周日| 120|

指定变量 $x_i,i\in{1,2,…,7}$ 表示从指定日期开始上班的人数，例如 $x_3=20$ 表示有二十个人从周三开始上班，每个工人都需要连续上五天班

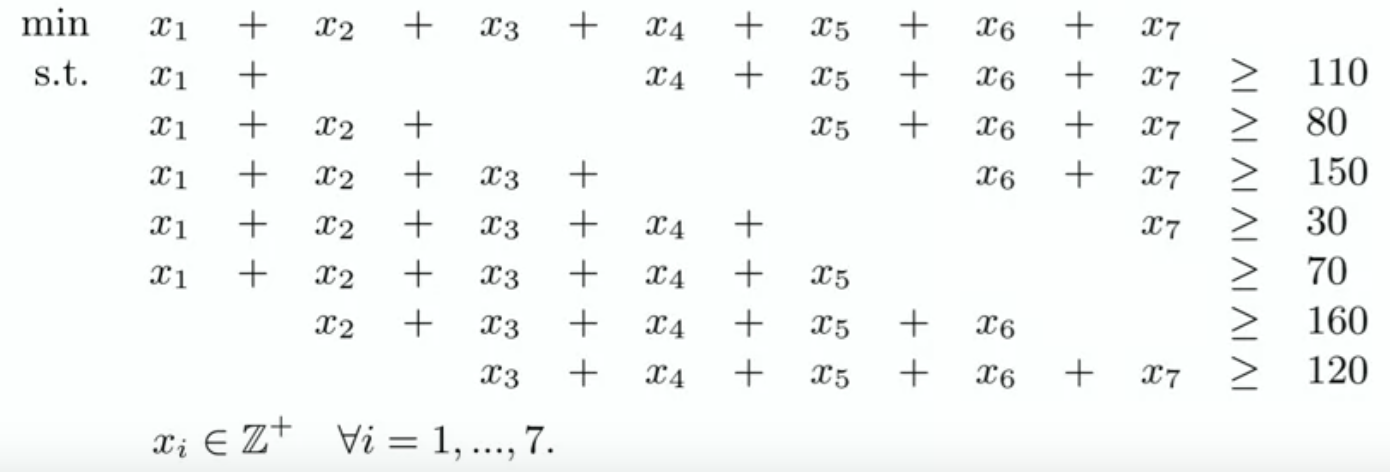
变量 $c_j=\sum x_i,j\in{1,2,…,7}$ 表示指定日期在岗上班的总人数

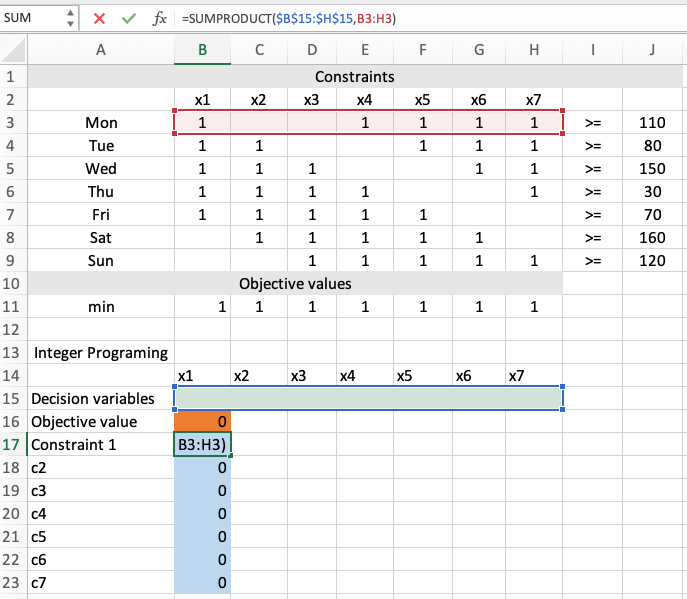
运行结果如下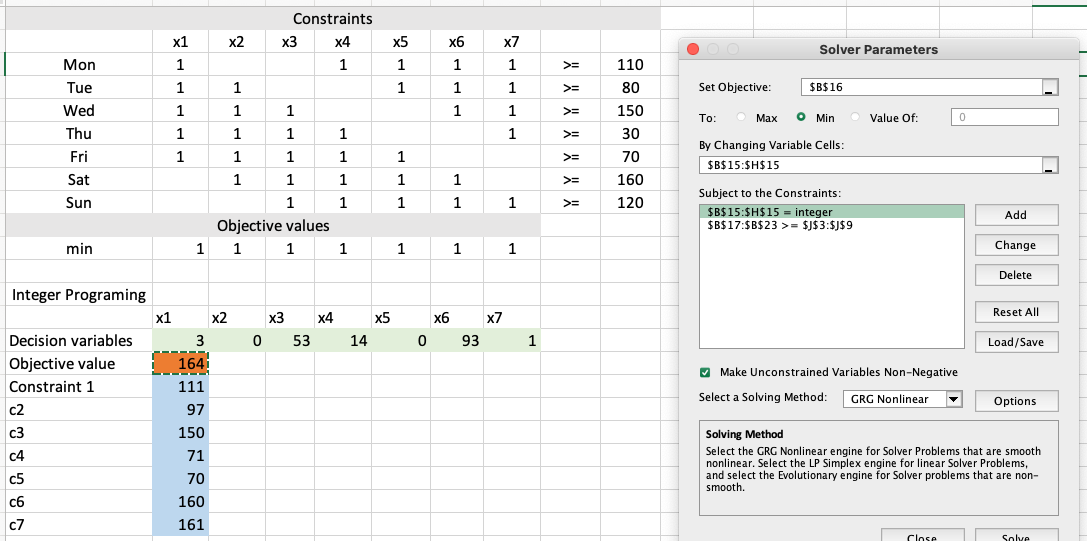

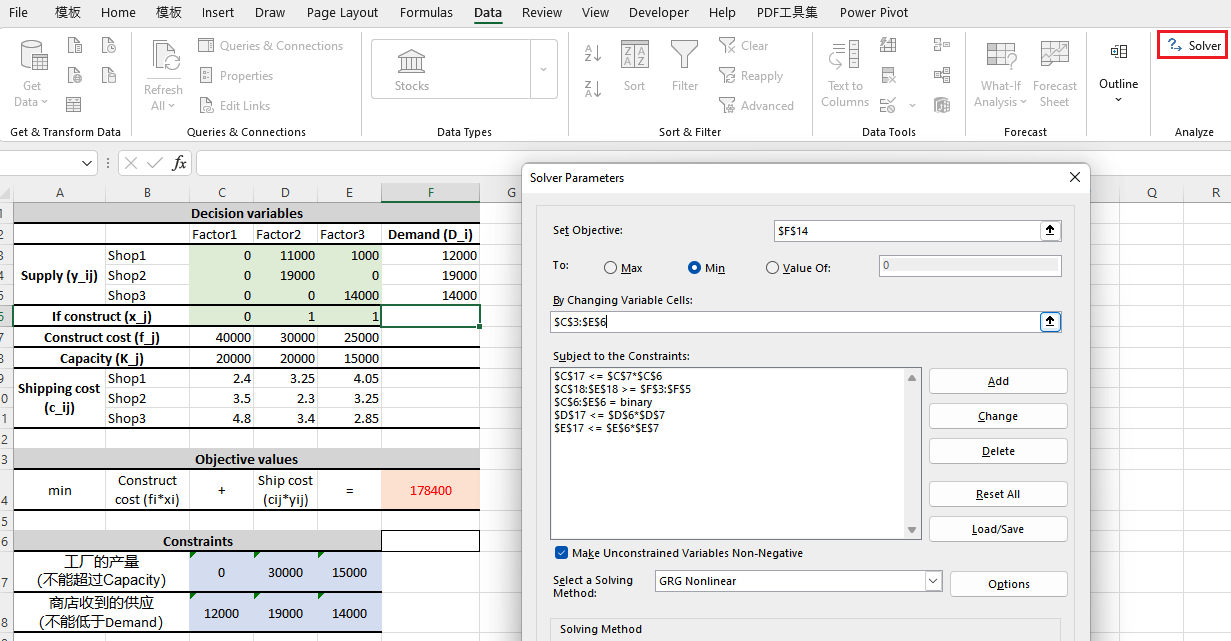
6.2 Ex: Facility location

Excel 示例: Excel: Integer Programming - Facility Location

使用 Matlab 求解 IP

相较于线性规划，”整数”这一限制难以在 Matlab 中约束

1 分支定界法

分支定界法主要由三步构成，分支、定界和剪枝：

1. 分支：根据线性规划的结果，把可行解空间反复分割为越来越小的子集。
2. 定界：对分支后的每个子集，使用线性规划计算其目标上界和下界。
3. 剪枝：每次分支后，凡是界限超出已知可行解目标值的子集不再进行进一步分支

1, 2 循环进行，并穿插 3，直到找到整数解。例如求解以下整数规划问题： \(\max\;z=40x+90y,\;\;s.t.\begin{cases} 9x+7y\leq56\\ 7x+20y\leq70\\ x,y\in N \end{cases}\)

下图展示了分支定界法的大致流程（该示例与上题无关）

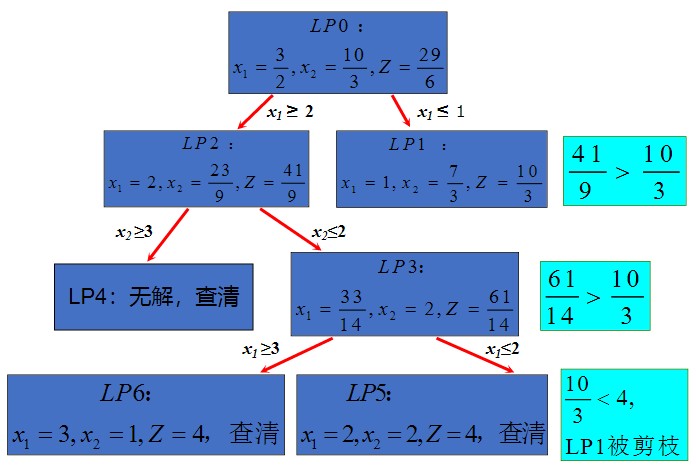
1.1 第一层分支：$B_1,B_2$

使用线性规划求最优解（非整数），可得 $x=4.81,y=1.82,z=355.88$

c = [40; 90];
A = [9, 7; 7, 20]; b = [56; 70];

x = linprog(-c, A, b, [], [], zeros(2,1))
value = c' * x

从而得到目标最优值的上下界 $z\in[0,356]$。利用 $x$ 进行分支（由于 4-5 之间不存在整数，故可忽略） \(x=4.81\to x\in[0,4]+x\in[5,\infty)\)

$B_1:$ \(\max\;z=40x+90y,\;\;s.t.\begin{cases} 9x+7y\leq56\\ 7x+20y\leq70\\ 0\leq x\leq 4\\ x,y\in N \end{cases}\)

$B_2:$ \(\max\;z=40x+90y,\;\;s.t.\begin{cases} 9x+7y\leq56\\ 7x+20y\leq70\\ x\geq 5\\ x,y\in N \end{cases}\)

1.2 对第一层定界

分别对 $B_1,B_2$ 使用线性规划求最优解（代码略），可得： \(\begin{aligned} & B_1: x=4,y=2.1,z=349\\ & B_2: x=5,y=1.57,z=341.43 \end{aligned}\)

此时更新目标最优值的上下界 $z\in[0,349]$

1.3 第二层分支：$B_{11},B_{12},B_{21},B_{22}$

同分支 1，此时可以利用 $y$ 进行分支： \(\begin{aligned} & B_1: y=2.1\to y\in[0,2]+y\in[3,\infty)\\ & B_2: y=1.57\to y\in[0,1]+y\in[2,\infty) \end{aligned}\)

从而得到新的分支 $B_{11},B_{12},B_{21},B_{22}$

1.4 对第二层定界

同 1.2， \(\begin{aligned} & B_{11}: x=4,y=2,z=340\\ & B_{12}: x=1.43,y=3,z=327.14 \end{aligned}\)

此时由于 $B_{11}$ 为整数解且其结果大于 $B_{12}$，可以直接剪掉 $B_{12}$（剪枝 1） \(\begin{aligned} & B_{21}: x=5.44,y=1,z=307.78\\ & B_{22}: \text{无解} \end{aligned}\)

同理，剪去 $B_{21}, B_{22}$（剪枝 2），并最终得到该整数规划的最优解 $B_{11}: x=4,y=2,z=340$

2 蒙特卡罗法

当解空间过大时，可以使用概率的方法随机选择部分解尽心验证，当随机解足够多是便能大概率获得最优解。例如求解以下非线性规划的问题：

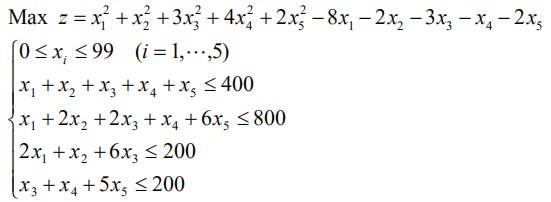
rng(sum(clock));  % 根据时间改变随机种子
p0 = 0;

for i=1:10^6
    x = 99 * rand(5,1);
	x1 = floor(x); x2 = ceil(x);
	[f,g] = mengte(x1);
    if sum(g<=0) == 4
        if p0 <= f
            x0 = x1; p0 = f;
        end, end
    [f,g] = mengte(x2);
    if sum(g<=0) == 4
        if p0 <= f
            x0 = x2; p0 = f;
        end, end
end

function [f,g] = mengte(x)
    % 定义 f 为目标函数值，g 为不等式约束（令规定 h 代表等式约束，不过此题没有）
    f = x(1)^2 + x(2)^2 + 3*x(3)^2 + 4*x(4)^2 + ...
        2*x(5) - 8*x(1) - 2*x(2) - 3*x(3) - x(4) - 2*x(5);
    g = [sum(x) - 400,
        x(1) + 2*x(2) + 2*x(3) + x(4) + 6*x(5) - 800,
        2*x(1) + x(2) + 6*x(3) - 200,
        x(3) + x(4) + 5*x(5) - 200];
end