References Coursera: Operations Research (1): Models and Applications (by National Taiwan University)
顾名思义,就是有着非线性的、高维的目标函数
1. Introduction
Ex: pricing a single good A product has purchasing price $c$, and selling price $p$ with selling amount $A(p)=a-bp$
- Parameters: $a,b,c$
- Decision variable: $p$
- Object: maximize profit
2. Economic Order Quantity (EOQ) Model
Look for order quantity that is the most economic, in other words, look for balance between odering cost and holding cost
Assumptions for basic EOQ model:
- Demand is deterministic and occurs at a constant rate
- Regardless order quantity, there is a fixed ordering cost
- Shortage is NOT allowed
- Inventory holding cost is contant
Ex: 某大型超市每年需要消耗600盏灯
已知条件如下:
- 每盏灯价格¥500
- 全年灯的消耗速率相同(例如每月消耗50盏)
- 每次不论购买多少灯,都需额外支付¥50订单费
- 每盏灯的 holding cost 为¥0.2每年
目标是最小化每年的总支出。需要探究的是 (1) 购买的频率 (2) 每次购买的数量
Parameters:
- $D$ annual demand (units)
- $K$ unit ordering cost (¥)
- $h$ unit holding cost per year (¥)
- $p$ unit purchasing cost (¥)
Decision variable: $q$ order quantity per order (units)
库存水平如下(灯的消耗速率恒定,并假设购买的频率和每次购买的数量不变),因此如果将范围扩大至很多年,不难得出 Average inventory level $=q/2$
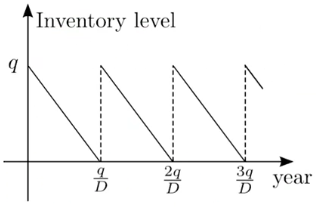
Annual Cost:
- Holding cost $=h\times (q/2)$
- Purchasing cost $=pD$
- Ordering cost $=K\times (D/q)$
Non-Linear Programming: Total cost should be the sum of three above, but since $pD$ is constant \(\min_{q\geq 0}\frac{hq}{2}+\frac{KD}{q}\)
3. Portfolio Optimization 投资组合优化
目标: 本金$100,000,求”最优”投资组合。这里的”最优”指的是在实现目标投资回报率的前提下最小化投资风险
将风险简单的定义为 Variance \(\text{Var}(X)=\sum_{i=1}^n\text{Pr}(X=x_i)(x_i-\mu)^2\)
| Stock | Current price | Expected future price | Unit variance |
|---|---|---|---|
| 1 | $50 | $55 | 100 |
| 2 | $30 | $50 | 1600 |
| 3 | $25 | $20 | 100 |
Decision Variables: 三个股票的购买数量 $x_1,x_2,x_3$
NLP: $R$ 表示目标投资回报额
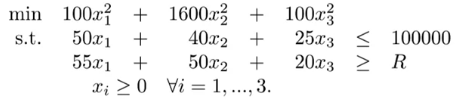
左图: 最优投资配比随着目标投资回报额升高而变化 右图: 总风险随着目标投资回报额升高而增大
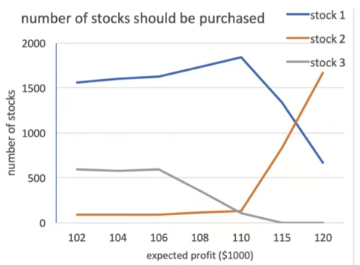
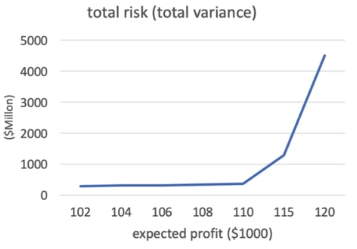
Compact formulation:
- Invest $B$ in $n$ stocks with min required expected revenue $R$
- For stock $i$, current price $p_i$, future price $u_i$, risk (variance) of buying one share $\sigma_i^2$
- Covariance between stock $i,j$: $\sigma_{ij}$
- Decision variables $x_i$ (shares of stock $i$ we buy)
4. NLP 的 Matlab 标准型
\(\underset{x}{\min}\;f(x),\;\;s.t.\begin{cases} Ax\leq b\\ Aeq\cdot x=beq\\ C(x)\leq 0\\ Ceq(x)=0 \end{cases}\)
where, $C(x),Ceq(x)$ 是非线性向量函数
% 完整形式
% NONLCON 为非线性约束条件
[x,y] = fmincon('func', x0, A, b, Aeq, beq, LB, UB, NONLCON, OPTIONS)
示例: 求解以下非线性规划问题
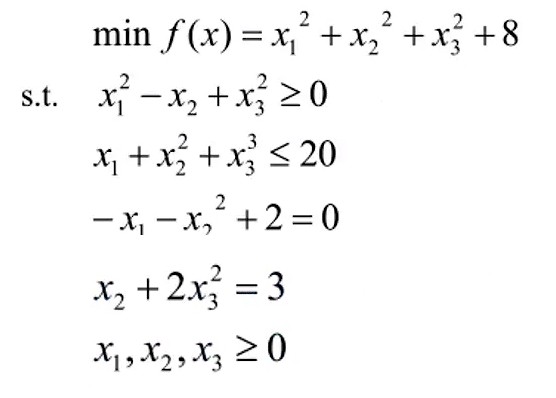
options = optimset('largescale','off');
[x,y] = fmincon('fun1',rand(3,1),[],[],[],[],zeros(3,1),[],'fun2', options)
function f = fun1(x) % 定义 f 为目标函数
f = sum(x.^2) + 8;
end
function [g,h] = fun2(x)
% 定义 g 为不等式约束,,h 为等式约束
g = [-x(1)^2 + x(2) - x(3)^2,
x(1) + x(2)^2 + x(3)^3 - 20];
h = [-x(1) - x(2)^2 + 2,
x(2) + 2*x(3)^2 - 3];
end
4.1 二次规划
二次规划为非线性规划中的一种,旨在解决目标函数为二次函数,但约束条件都是线性的非线性规划问题
\(\min\frac{1}{2}x^THx+f^Tx,\;\;s.t.\begin{cases} Ax\leq b\\ Aeq\cdot x=beq \end{cases}\)
[x,fval] = quadprog(H, f, A, b, Aeq, beq, LB, UB, x0, OPTIONS);
示例: 求解以下二次规划问题
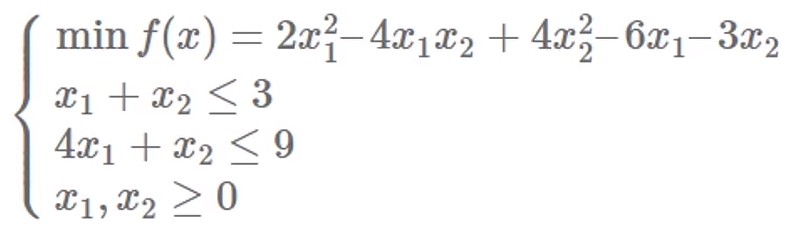
h = [4,-4;-4,8];
f = [-6;-3];
a = [1,1;4,1];
b = [3;9];
[x,value] = quadprog(h,f,a,b,[],[],zeros(2,1))
Document Information
- Author: Zeka Lee
- Link: https://zhekaili.github.io/0005/01/03/nonlinear-programming/
- Copyright: 自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)