Case Study: Call Center Personnel Scheduling

1. Background and Motivation

目标: 分配 CSR (customer service representatives 即客服人员) 来满足用户 call-in 的需求。通过设定 desired service level 来定义目标需求，例如 level=95% 表示至少有该比例的 call-in 被接听

根据历史数据，已知每个工作日每个时段 call-in 的大致数量

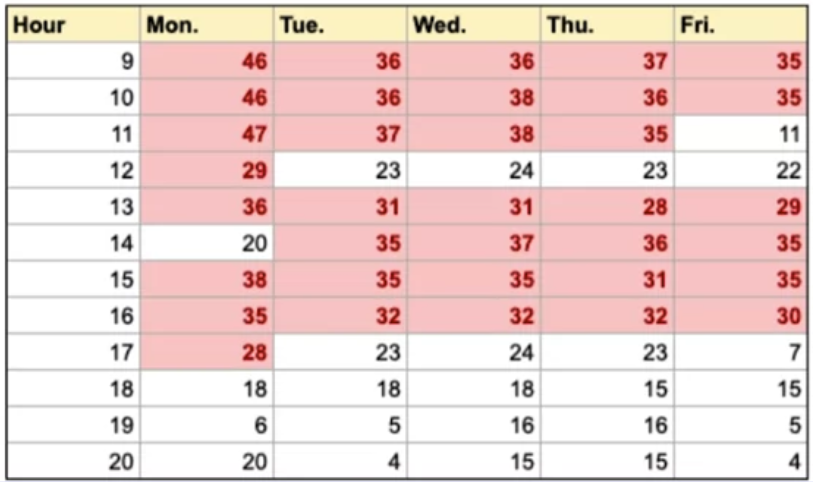
然而由于以下原因 scheduling is difficult:

• 每个接线员在一天内工作时间必须是连续的
• 每个接线员一周内最多只能上一天夜班
• 每个时间段必须有至少一名 manager
• …

由于诸如此类的原因，手动分配往往会造成很大人员的冗余。因此我们需要 schedule with operations research

2. Schedule with Operations Research

It’s an allocation problem $\to$ Linear Programming

• #CSRs is limited (接线员总人数有限)
• try to minimize total shortage (尽可能提升 service level)

It’s a selection problem $\to$ Integer Programming

• 如果一个接线员上了白班，那就不能继续上当天的夜班
• 每个接线员一周内最多只能上一天夜班

3. Problem Description (use IP)

3.1 Decisions

D1: 对于每个接线员，告诉她们下个月在哪几天工作、哪几天休息 D2: 对于每个接线员的每个工作日，告诉她们工作开始、中途休息以及工作结束的时间

In practice, use shifts to define work hours. For example:

• Shift 1: 8:00-17:00 with lunch break 12:00-13:00
• Shift 2: 8:30-17:30 with lunch break 12:30-13:30
• …
• Shift 0: a day off

例如下图展示了 Shift 0-15:

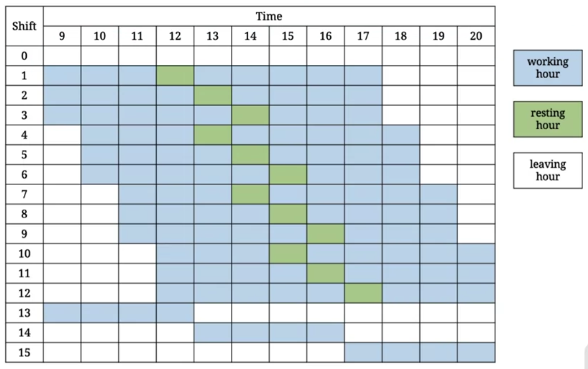
这样一来就把开头的两个 decisions 转化成了一个 shifts 分配问题: assign one shift to each CSR for each day

3.2 Objective

Minimize total shortage (尽可能提升 service level), define \(\text{shortage}=\max\{\text{Total CSRs on duty}-\text{Demand},0\}\)

例如对于下图 shifts 的分配方式，total shortage 等于最后一行的求和

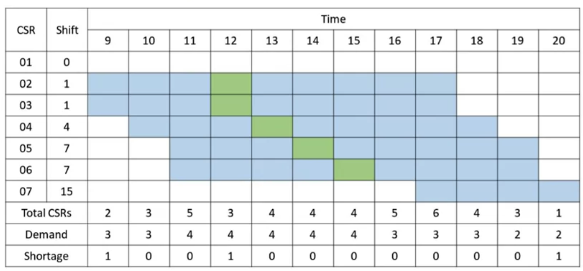
3.3 Constraints

Hard constraints (must satisfy):

• Each CSR should be assigned to exactly one shift per day
• Each CSR should be assigned to at most one night shift(a shift contains work after 18:00) per week
• …

Soft constraints (nice to have):

• Fairness among periods: rather than having 5 extra CSRs in period 1 and only 1 extra CSR in period 2, it is better to have 3 extra CSRs in each period
• Fairness among CSRs: each CSR should have similar night-shifts per month

4. Model Formulation

4.1 Varaibles

Notations $i\in I$ denotes $i$th CSR $j\in J$ denotes $j$th day in the next month $k\in K$ denotes $k$th work shift $t\in T$ dnotess 工作日的 $t$th 个时刻，例如对于 9:00-20:00 这样的工作时长，$t=2$ 表示 10:00-11:00

Decision Variables \(x_{ijk}=\begin{cases} 1 & \text{if CSR }i\text{ is assigned to shift }k\text{ in day }j \\ 0 & \text{otherwise} \end{cases}\)

Derived variables: \(y_{jt}=\text{\#CSR shortage in period }t\text{ of day }j\)

4.2 Objective function

The objective function should include the major objective(minimize total shortage) and two soft constraints(fairness among periods and CSRs)

• $w_1$: max number of extra on-duty CSRs among all periods 最大服务冗余
• $w_2$: max number of night-shifts among all CSRs 最多夜班数量

where $P_0,P_1,P_2$ are weights determined by manager

4.3 Constraints

(1) For each day, each CSR should be arranged one shift \(\sum_{k\in K}x_{ijk}=1\;\;\;\;\forall j\in J,i\in I\)

(2) #CSR shortage in period $t$ of day $j$ \(y_{jt}\geq D_{jt}-\sum_{k\in K}A_{kt}\sum_{i\in I}x_{ijk}\;\;,\;\;y_{jt}\geq 0\;\;\;\;\forall j\in J,t\in T\)

where

• $A_{kt}=1$ 表示 shift $k$ 包含了时刻 $t$，反之为零
• $D_{jt}$: #CSRs needed in period $t$ of day $j$

(3) $w_1$ max mumber of extra on-duty CSRs among all periods, all days       $w_2$ max number of night-shifts among all CSRs \(w_1\geq \sum_{k\in K}A_{kt}\sum_{i\in I}x_{ijk}-D_{jt}\;\;\;\; \forall j\in J,t\in T\)

where $K^N\subset K$ is the set of night shifts

**(4) **