Row and Column Views for a Linear System

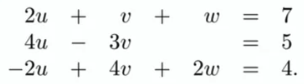
例如对于如上等式组:

• Row view: 求三个面的交点
• Coluimn view: 三向量的合成向量 $x_1u+x_2v+x_3w=y$

Singular Cases: 等式组有无穷解或无解

• Row view: 三个面相较于一条线(无穷解); 双面平行、三面交三线、三面平行(无解)
• Column view: 三个向量只能形成一个平面或一条线，这样目标点其内有无数解，在其外则无解

Gaussian Elimination to solve Ax=b

高斯消元法:

• Elimination: 第 2-n 行减去第1行的倍数使得第 2-n 行的首元素为0，第 3-n 行减去第2行的倍数使得第 3-n 行的第二个元素为0…直至变成一个上三角矩阵
• Back Substitution: 从第n行开始消到第1行, 直至变成一个对角矩阵

Time Complexity: $O(n^3)$

• Elimination: 对第一行的 elimination，剩下的 n-1 行都需要做 n+1 次操作(包括等号右侧的元素)，因此共 (n+1)(n-1) 步；对第二行的 elimination, 共 (n)(n-2) 步… 总共 $n^3/3+n^2/2-5n/6\to n^3/3$ 步
• Back Substitution: 总共 $n^2/2$

Gauss-Jordan Elimination to find A^(-1)

该方法求逆矩阵的步骤与高斯消元法非常类似: \([\;A\;\vert\;I\;]\to[\;I\;\vert\;A^{-1}\;]\)

时间复杂度也同样是 $O(n^3)$

Linear Dependence and Independence

m 个 n 维向量 $x_1,…,x_m$ are linearly dependent 如果存在一个向量 $m\in\R^m$ \(w_1x_1+...+w_mx_m=0\)

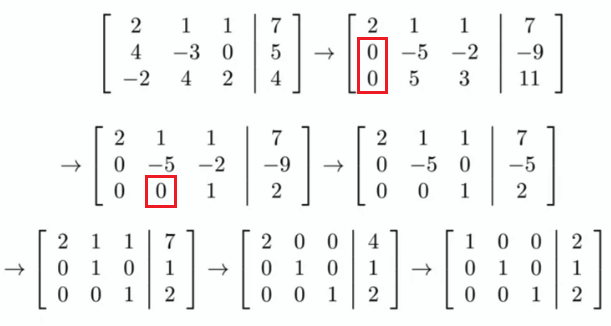
使用高斯消元来判断 if dependent: 例如对于以下三个三维向量

• 如果高斯消元后仍存在三个 pivots 则这三个向量 linearly independent
• 反之如果 pivot 的个数小于三个，则 linearly dependent

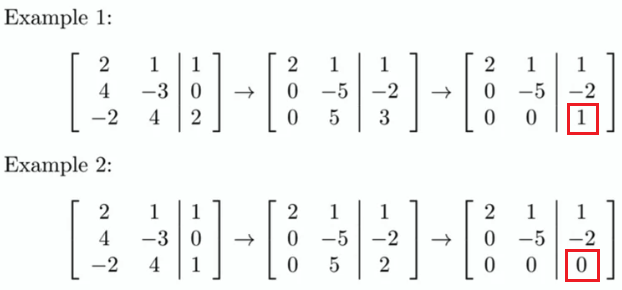
Standard Form of LP

Definition 1 (Extreme Points)

In an area set $A\in\R^n$, a point $x$ is an extreme point 如果不存在 $x_1,x_2\in A$, $\lambda\in\R$ 满足 $x=\lambda x_1+(1-\lambda)x_2$. 例如下图中黑色顶点以及半圆形的整条弧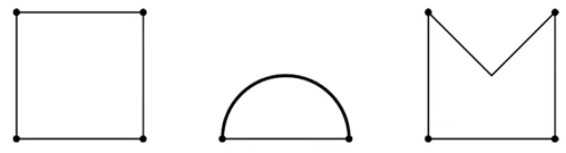

Proposition 1 For any LP, if there is an optimal solution, there is an extreme point optimal solution 反之不成立，也不意味着一个 optimal solution 一定是个 extreme point

Definition 2 (Standard Form of LP)

An LP is in the standard form if:

• all RHS (right hand side) values >= 0
• all variables >= 0
• all constraints are equalities

Requirement 1: all RHS >= 0 \(2x_1+3x_2\leq -4\implies -2x_1-3x_3\geq 4\)

Requirement 2: all variables >= 0

• if $x_i$ is nonpositive, replace it by $-x_i$ \(2x_1+3x_2\leq4,x_1\leq0\implies -2x_1+3x_2\leq4,x_1\geq0\)
• if $x_i$ is free, replace it by $x’_i-x’‘_i$ where $x’_i,x’‘_i\geq 0$ \(2x_1+3x_2\leq4\implies 2x'_1-2x''_1+3x_2\leq4,x'_1,x''_1\geq0\)

Requirement 3: all constraints are equalities

• For $\leq$, add a slack variable \(2x_1+3x_2\leq4\implies 2x_1+3x_2+x_3=4,x_3\geq0\)
• FOr $\geq$, minus a surplus variable \(2x_1+3x_2\geq4\implies 2x_1+3x_2-x_3=4,x_3\geq0\)

Example: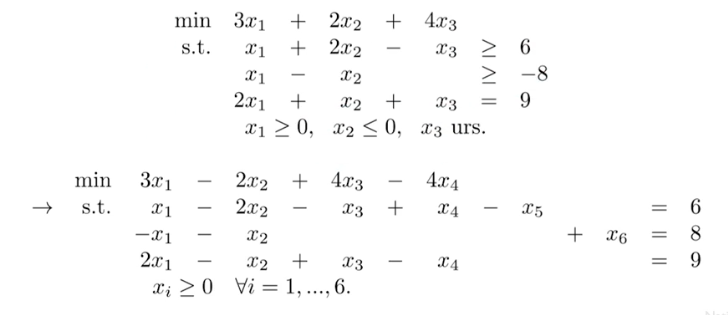

Standard Form of LPs in Matrices

\(\min\;\;c^Tx\)

where $x_{n\times 1}$ is the variable

• $A_{m\times n}$ is the coefficient matrix
• $b_{m\times 1}$ is the RHS vector
• $c_{n\times 1}$ is the objective vector

Definition 3 (Basic solution)

Consider a standard form LP with $m$ constraints and $n$ variables. Assume $A$ has $m$ pivots, i.e., all rows of $A$ are independent

这意味着 $m\leq n$。又因为当 $m=n$ 时 A 为方阵，此时只有唯一解 $x=A^{-1}b$。因此不妨直接假设 $m\leq n$

Definition 3 (Basic solution) A basic solution to a standard form of LP must (1) has $n-m$ variables = 0 (2) satisfy $Ax=b$

Denotations:

• $x_N\in\R^{n-m}:n-m$ variables chosen to = 0 are nonbasic variables
• $x_B\in\R^m:$ remaining $m$ varaibles are basic variables
• the set of basic variables is called a basis
• $A_B:$ a nonsigular(invertible) $m\times m$ matrix formed by $m$ columns of $A$

therefore, we have $x_N=0$ and $x_B=A_B^{-1}b$

由于一个 basis 由 $n$ 个 variables 中的 $m$ 个组成，因此至多有 $\begin{pmatrix} n
m \end{pmatrix}$ 个不同的 bases

Example:

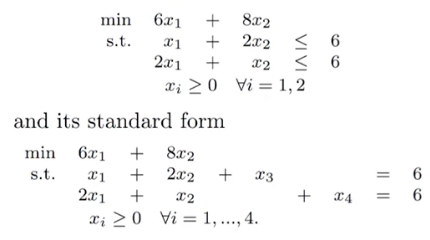
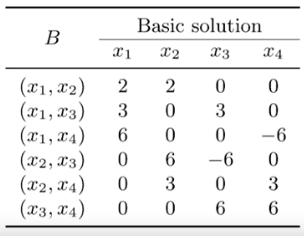
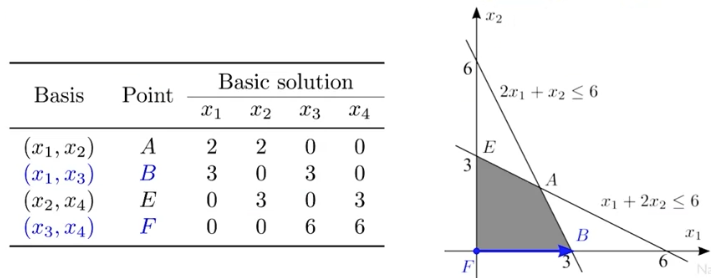
Definition 4 (Basic Feasible Solutions)

基于 basic solutions, basic feasible solutions 还需要满足所有 varaibles >= 0 (Definition 2-Requirement 1)。例如上图中的第三、四个 basic solutions 就不是 basic feasible solutions

Theorem 1 (Extreme Points and Basic Feasible Solutions) For a standard form LP, a solution is an extreme point of the feasible region $\iff$ it’s a BFS to the LP

Theorem 2 (Optimality of Basic Feasible Solutions) For a standard form LP, if there is an optimal solution, there is an optimal BFS

One-to-one mapping between BFS and extreme points: 其中 $x_1,x_2$ 体现各 solution 的实际坐标，$x_3,x_4$ 为 slack variables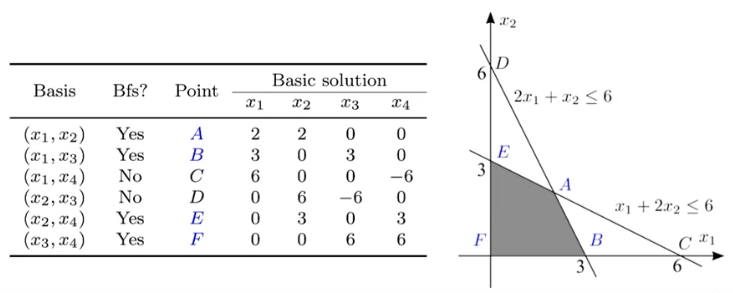

Definition 5 (Adjacent BFS)

从图形化的角度看，通过遍历所有 extreme points 即可找到 optimal solution. 但是对于算法而言遍历图形化的点是非常复杂的，因此 we search among all BFS instead of extreme points

那么如何 search among all BFS? 从任一 bfs 出发，keep moving to find a better adjacent BFS

Definition 5 (Adjacent BFS) Two bases are adjacent if exactly one of their variables is different Two BFS are adjacent if their associated bases are adjacent 体现在下图中，一对 adjacent BFS 对应一对 extreme points（在同一条边上）；而从一个 BFS 移动到其任一 adjacent BFS 相当于在域的边上移动

The Simplex Method

进一步的，我们现在的目标是通过不断的 move to a better adjacent BFS 直至找到 optimal solution. 这一过程中有两个关键:

• 首先是判断 How to move to an adjacent BFS
• 其次是判断 Where to move(e.g. which adjacent is better) 以及 When to stop

How to move

核心是 Entering and Leaving，以上图中的移动 $F\to B$ 为例:

• 对于 $B$ 点: $x_1,x_3$ 为 basis(basic variables), 而 $x_2,x_4$ 为 nonbasic variables
• Entering: 选择一个 nonbasic variable, $x_4$, to become basic, 也就是把 $x_4$ 的数值从零涨到一个正数
• Leaving: 当 $x_4$ 上涨时，为了满足 $Ax=b$，某些原来的 basic variables 会下降。这里我们选择那个最先下降到零的 basic variable, $x_1$, to become nonbasic

Where to move

MAX objective function:

Example (1)

为 objective function 引入 $z$，为两个 constraints 引入 $x_3,x_4$ \(\max\;\;z\)

(1) Start from a BFS 这题的 starting BFS 非常明显，直接选择 $(x_3,x_4)$, 转化成 Tablua Form 如下:

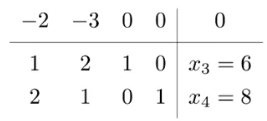
The first BFS is $x^{(1)}=(0 ,0,6,8)$ with $z^{(1)}=0$

(2) Entering and Leaving 现在有两个系数为负的 nonbasic variables $x_1,x_3$

(2.1) Which to enter? 首先我们的 objective function 为 MAX，因此我们需要 enter 一个系数为负数的 nonbasic variables. $x_1,x_2$ 的系数均为负数，那就任意选一个，assume choose $x_1$ to enter

(2.2) Which to leave? 在 $x_1$ enter 后，两个 constraints 变成了: \(\begin{cases} x_1 + x_3&=6\\ 2x_1 + x_4&=8 \end{cases}\)

此时当 $x_1$ 逐渐从零开始变大，$x_4$ 会更早低变成零(become nonbasic)，先于 $x_3$. 因此 leave $x_4$

(3) Update Tabula 因为选择 enter $x_1$ leave $x_4$ 因此 pivot 行就是 $x_4$ 对应的的第二行，pivot 元素就是该行对应 $x_1$ 的第一个元素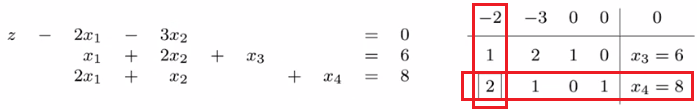

首先把 pivot 元素变成 1，然后将其他行的对应元素消除，完成后效果如下:

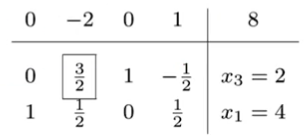
The second BFS is $x^{(2)}=(4,0,2,0)$ with $z^{(2)}=8$

(4) Repeat (2) & (3) 第一次更新完后两个 nonbasic varaibles $x_2,x_4$ 的系数一正一负

因为是 MAX 问题，一次选择负系数的 $x_2$ enter. 此时两个 constraints 变成了: \(\begin{cases} \frac{3}{2}x_2 + x_3&=6\\ 2x_1 + \frac{1}{2}x_2&=8 \end{cases}\)

因为 $8/(\frac{1}{2})>6/(\frac{2}{3})$，因此 $x_3$ 会更快地变零 $\to$ 选择 leave $x_3$

因为选择 enter $x_2$ leave $x_3$ 因此 pivot 行就是 $x_3$ 对应的的第一行，pivot 元素就是该行对应 $x_2$ 的第二个元素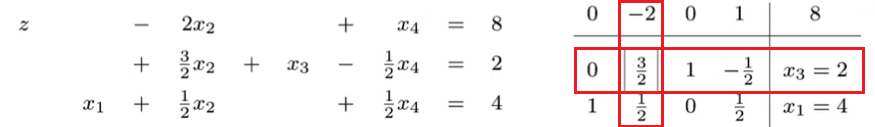

首先把 pivot 元素变成 1，然后将其他行的对应元素消除，完成后效果如下:

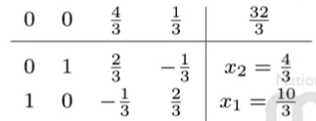
The third BFS is $x^{(3)}=(\frac{10}{3},\frac{4}{3},0,0)$ with $z^{(3)}=\frac{32}{3}$

(5) Stop and Find Optimal 第二次更新完后有两个系数为零的 basic variables $x_1,x_2$, 和两个系数为正的 nonbasic variables $x_3,x_4$。因为是 MAX 问题，系数为正的 nonbasic variable 在 enter 之后反而会使 objective function 下降，这意味着 stop moving & find the optimal solution

The optimal BFS is $x^{()}=(\frac{10}{3},\frac{4}{3},0,0)$ with $z^{()}=\frac{32}{3}$