1. Intro

Consider perishable items such as fruits

• These perishable items should be removed at the end of each single period
• Getting rid of leftover items may cost money. Even if there is any positive salvage value, it is smaller than the ordering cost
• If order too many items, there will be many left-over items.
• If order too few, we lose potential sales.

Newsvendor problem is to find the ordering quantity that maximizes profit or minimizes cost.

2. Notation and Problem

• $D_i=$ demand at period $i$ (r.v.)
• $q=$ ordering quantity
• $P(D,q)=$ profit for one period when we order q and demand is D;
• $C(D,q)=$ cost for one period when we order q and demand is D;

Since $D_i$ is a r.v., we cannot solve $\max_q P(D_i,q)$.

Instead, if during $n$ periods ($n$ is large), the distribution of $D_i$ does not change and we order the same quantity $q$ every period, we can solve: \(\max_{q} \frac{1}{n}\sum_{i=1}^n P(D_i,q)=E[P(D,q)]\)

(equality keeps because of SLLN(Strong law of large number))

Equally, minimizing cost is equal to maximizing benefit, therefore we have \(\boxed{\min_q E[C(D,q)]}\)

3. Discrete Demand

As $E[C(D,q)]$ is a function of $q$ only, we denote $g(q)=E[C(D,q)], \Delta=g(q+1)-g(q)$

From the following picture, we have \(\text{Find q*}\iff\text{Find first q that make }\Delta\geq 0\)

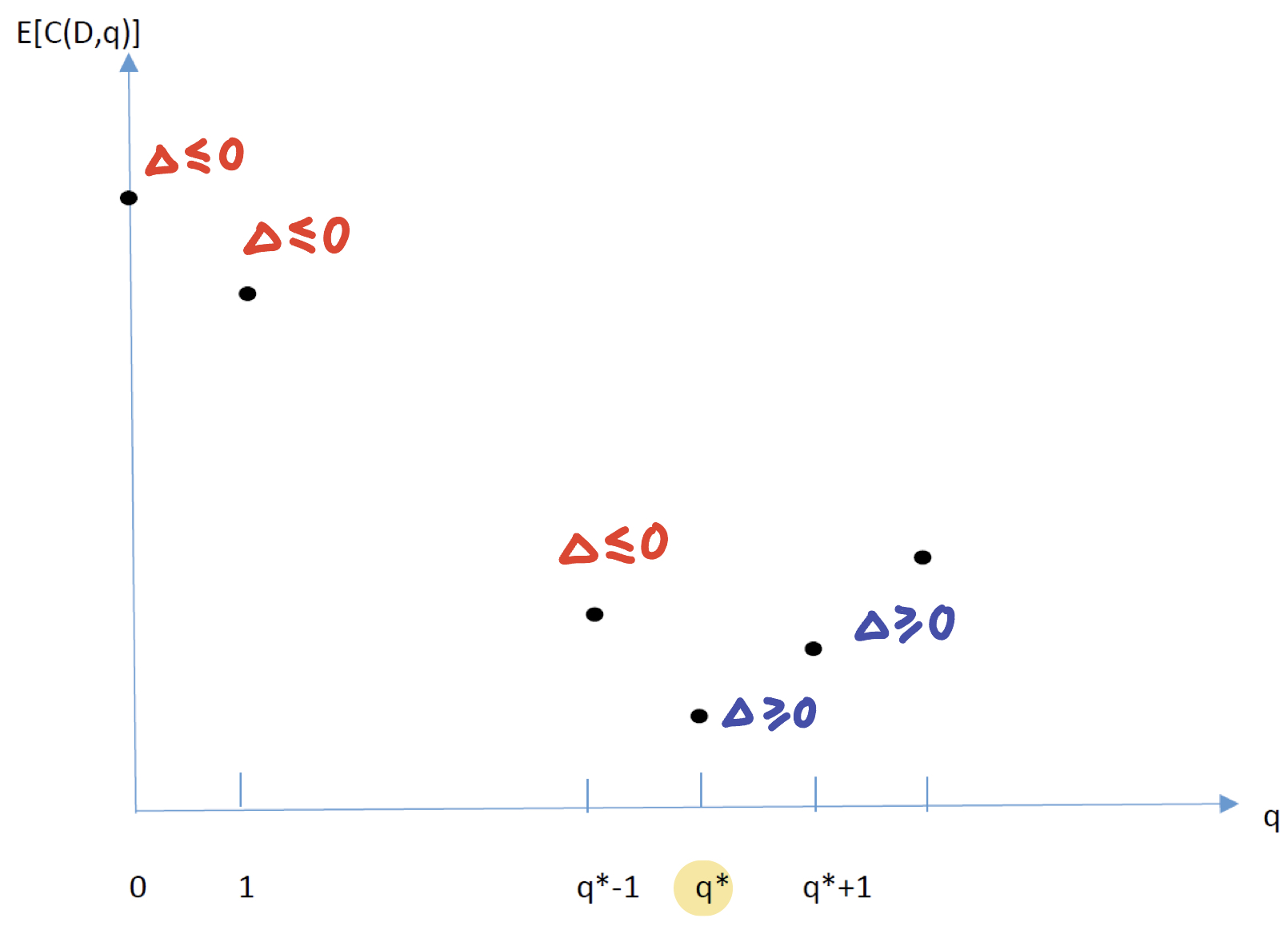
Marginal Analysis (1) If $d\leq q$, overstock: $C_1(d,q)=c_oq+(p_1d+k)$ (2) If $d> q$, understock: $C_2(d,q)=-c_uq+(p_2d+k)$

• $c_o$ is called overage cost: how much do we lost when ordering one more item in overstock case
• $c_u$ is called underage cost: how much do we gain when ordering one more item in understock case

Example: 报纸进货价 $0.5, 售价 $1.5. 每周的需求 $d$ 分布如下，剩下没卖完的报纸直接扔掉

• If $d\leq q$, overstock: $C_1(d,q)=0.5q-1.5d$
• If $d>q$, understock: $C_2(d,q)=0.5q-1.5q=-q$

Therefore we have $\boxed{c_o=0.5,c_u=1}$

Newsvendor Ratio Accroding to the definition of $c_o,c_u$ \(\Delta = g(q+1)-g(q) = E[C(D,q+1)-C(D,q)]=\begin{cases} c_o &\text{if }q\leq d\\ -c_u &\text{if }q>d \end{cases}\)

\[E[\Delta]=c_oPr(D\leq q)-c_uPr(D>q)=c_oF(q)-c_u(1-F(q))\]

这里有必要说明一下，因为上图中的函数是 $E[C(D,q)]$，所以它的导数为 $E[\Delta]$ 而不是 $\Delta$

When $E[\Delta]$ firstly reach 0 as $q$ increasing, we call the accroding $F(q)$ as Newsvendor Ratio \(\boxed{F(q^*)=\frac{c_u}{c_o+c_u}}\)

因此第一个使 $F(q)$ 大于 Newsvendor Ratio 的 $q$ 即为 $q^*$

Example continous: |$d$|20|25|30|35 |-|-|-|-|-| |$p(d)$|0.1|0.2|0.4|0.3 |$F(d)$|0.1|0.3|0.7|1

Since $F(q^)=c_u/(c_o+c_u)=2/3$, we find that $\boxed{q^=30}$ is the first time that make $F(q)>2/3$

4. Continuous Demand

与 Discrete Demand 相同，即通过 $C_1(q,q)=C_2(q,q)$ 可得: \(q^*=F^{-1}\Big(\frac{c_u}{c_o+c_u}\Big)\)

然后再四舍五入取整. 计算 expected cost: