Berth or berthing areain a seaport is where ships are moored for unloading and loading operations

1. Parameters

For Berth Allocation Problem (BAP)

• Given:
  • berth layout of a container terminal
  • $V$: set of vessels to be served within a planning horizon
  • $a_k,p_k$: vessel $k$’s arrival time and proccessing time
  • $h_k$: vessel $k$’s length
  • $d_k$: due date of vessel $k$
• Decide:
  • $t_k\geq a_k$: berthing time for each vessel
  • $c_k=t_k+p_k$: completion time of vessel $k$
  • $b_k$: berthing position for each vessel

Such that a given objective function is optimized.

2. Discrete Single Berth Scheduling

2.1 Scheduling Objectives

(1) MS: Makespan How long until all works finish? \(\min\max_{k\in V} c_k\)

(2) TCT: Total Completion Time \(\min\sum_{k\in V}c_k\)

2.2 Case 1: $a_k=0$ (Easy)

MS: $\max c_k=\sum p_k$

TCT: sort jobs by $1/p_1 \geq 1/p_2\geq …\geq p_n$ (For weighted case, just sort by $w_k/p_k$)

2.3 Case 2: $a_k\neq 0$ (use MIP)

MIP (Mixed-Integer Programming)

Primary scheduling variable $x_{kl}\in {0,1}$

• $x_{kl}=1$ iff vessel $k$ is completed before $l$
• which means if $x_{kl}=1$, then $t_l\geq t_k+p_k=c_k$
• therefore we can combine them into constraint one:

Other constraints: \(\tag{2}x_{kl}+x_{lk}\geq 1\)

这里的大于等于相当于使用等号，因为大于1的情况会被上面的约束排除

3. Linear Berth Scheduling

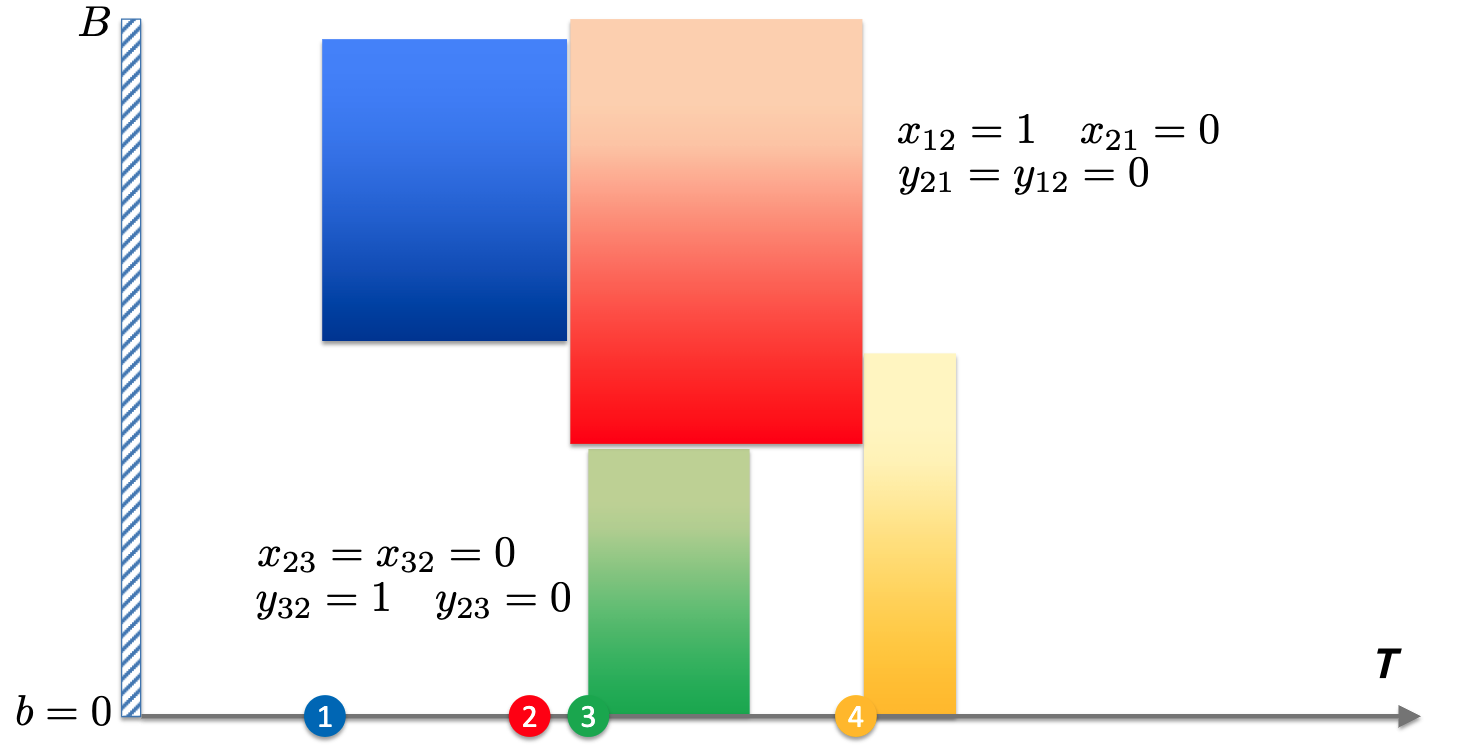
Primary scheduling variable $x_{kl}, y_{kl}\in {0,1}$

• $x_{kl}=1$ iff vessel $k$ is completed before $l$
• $y_{kl}=1$ iff vessel $k$ is completely under $l$

Ex: TCT Problem

\(\min \sum_{k\in V}c_k\)

• $x_{kl}+x_{lk}+y_{kl}+y_{lk}\geq 1$
• $t_l\geq t_k+p_k+M(x_{kl}-1)$
• $t_k\geq a_k$
• $c_k=t_k+p_k$
• $b_l\geq b_k+h_k+M(y_{kl}-1)$
• $b_k\geq 0$
• $b_k\leq B-h_k$

The first constraint is the key to avoid overlapping in both time and space (we have no overlap or only one overlap)

4. Multiple Berths Scheduling

现在不仅需要分配时间 $t_k$，还需要把 vessels 分配给每个 berth。理论上我们需要引入变量 $\beta_k\in {1,2,3,…}$ 来表示 vessel $k$ 属于第几个 berth。

但是有一种很巧妙的方式，使用两个 binary variable 来代替 $\beta_k$:

• $\boxed{w_k=1}$ iff vessel $k$ is first process at some berth
• $\boxed{x_{kl}=1}$ iff vessel $k$ immediately precedes $l$ at the same berth
• 这里我们不在乎每个 vessel 到底停在哪个 berth，而是用以上两个变量创建一种类似 linked list 的结构:
  • $w_k=1$ 说明 $k$ 是一条链的表头
  • $x_{kl}=1$ 说明 $l$ 在某条链中紧跟在 $k$ 后面
  • 
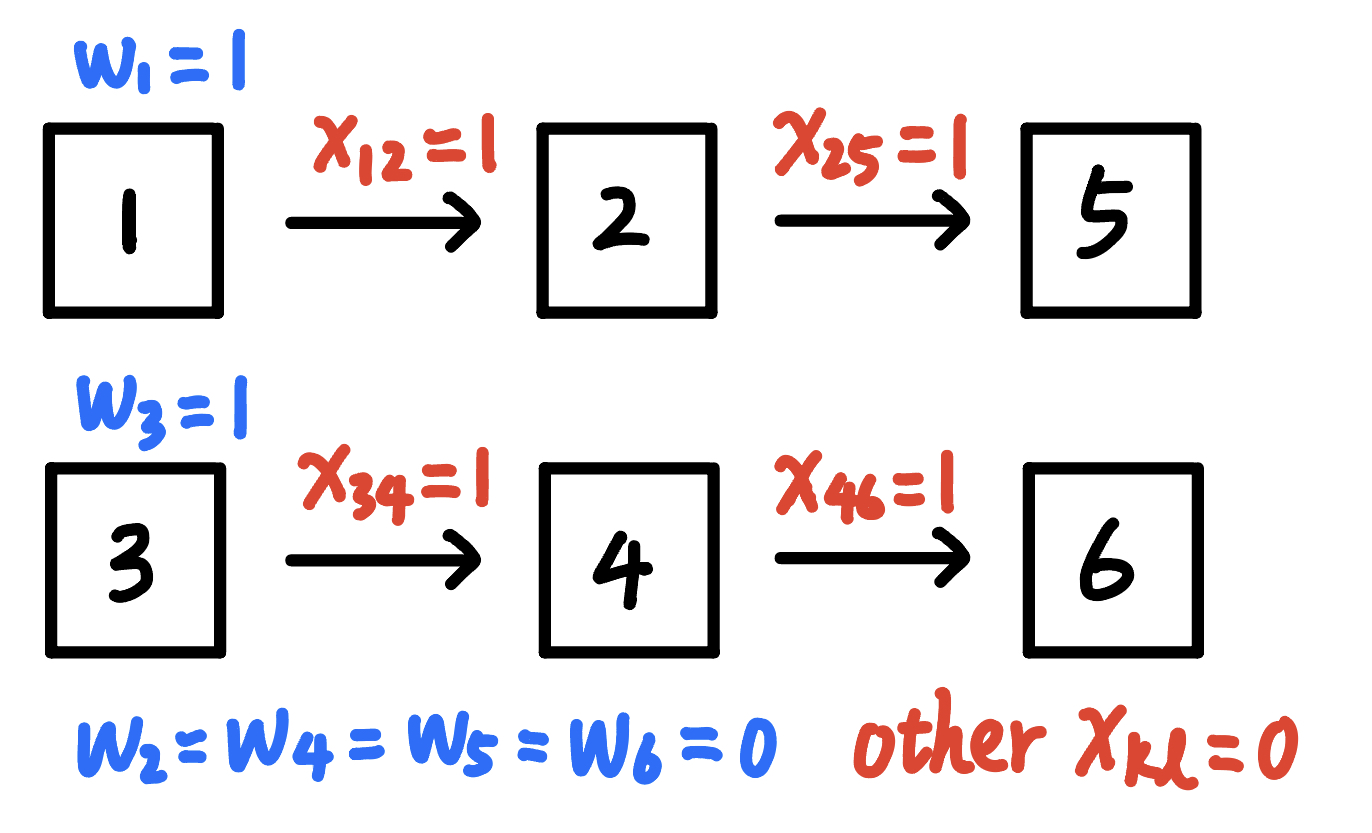
• Such kind of relative position variables can create stronger lower bounds

Constraints:

• $w_l+\sum_{k\neq l}x_{kl}=1$ (vessel $l$ 要么作为开头要么跟在 $k$ 后面)
• $\sum_{l\neq k}x_{kl}\leq 1$ (每个 vessel 最多只能 immediately precedes 一个 vessel)
• $\sum_k w_k\leq \Beta$ (constraint of the number of berths)

5. Headway and Flows

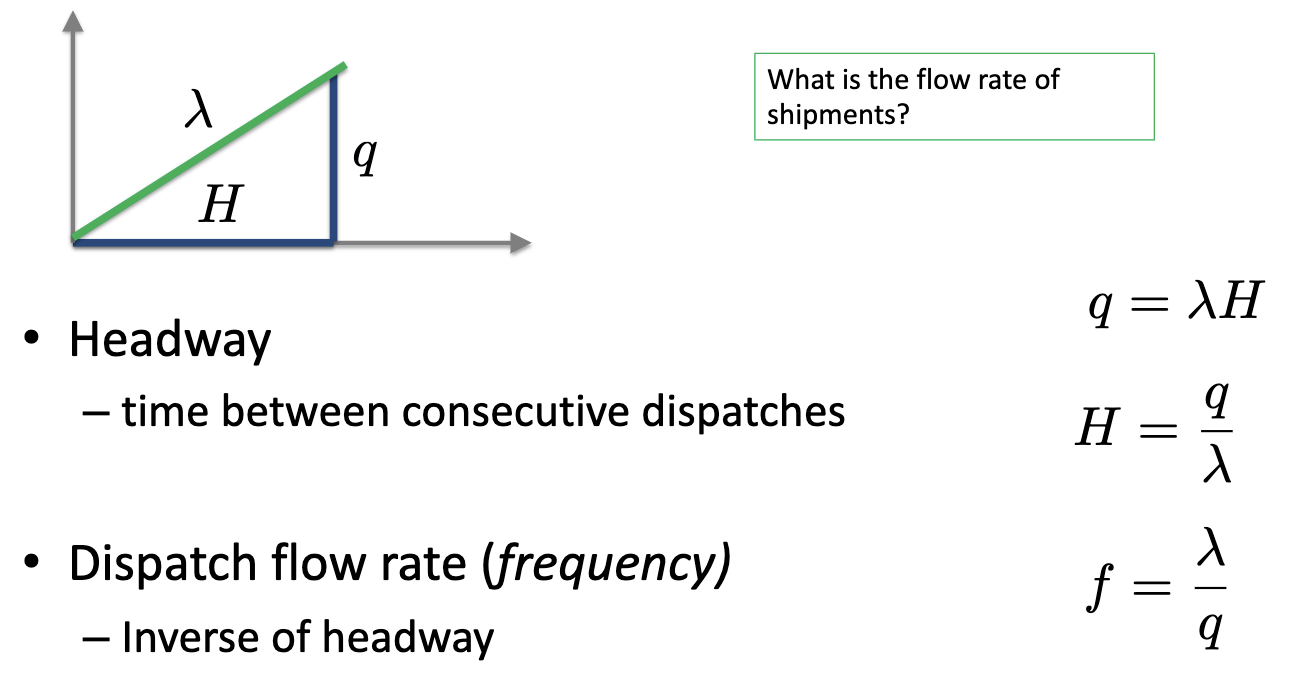
• $\lambda$: average flow rate (production rate)

To find the minimum frequency, choose the maximum shipment size, i.e. let $q=Q$

5.1 Cyclic dispatch fleet sizing

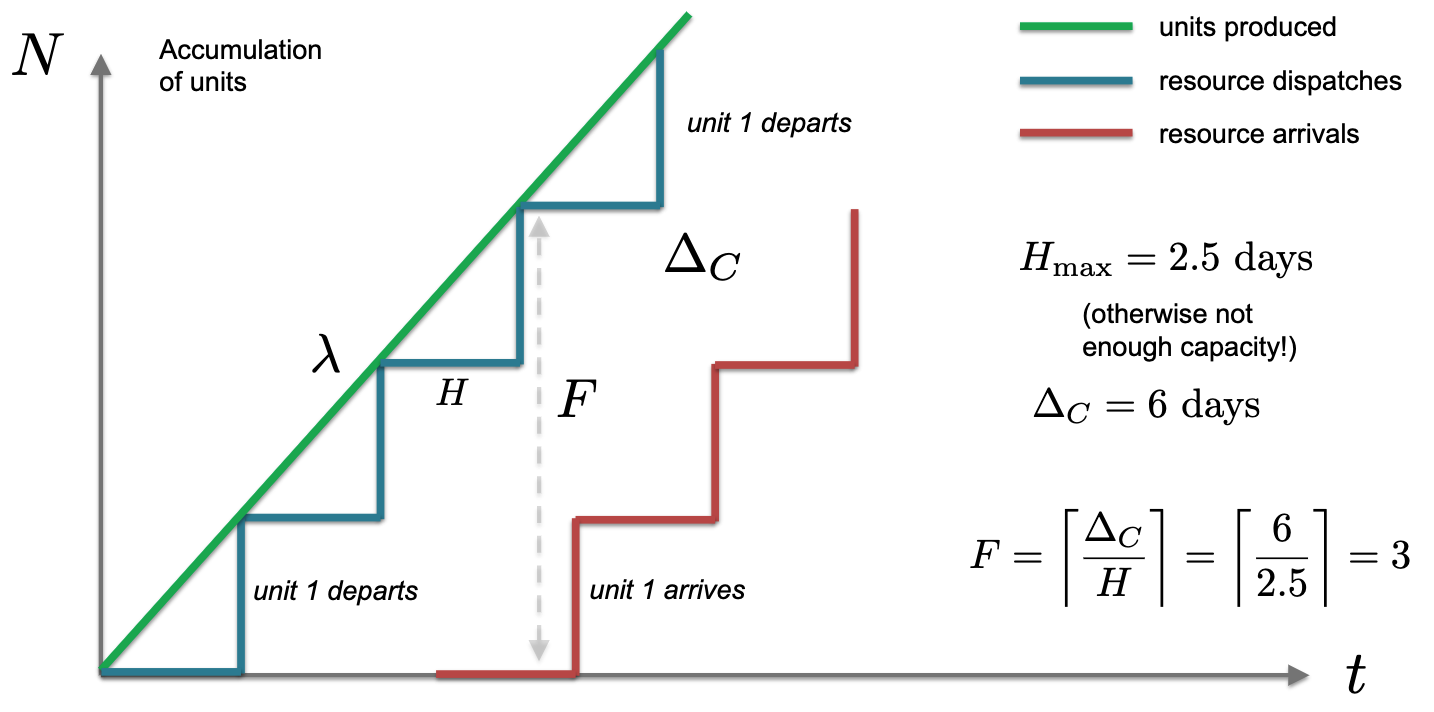
• $H$: headway
• $\Delta_C$: time need to finish a cycle (from departure to ready-to-departure)
• $F$: fleet size (number of vessels needed)

5.2 Waiting time

In the case above, every vessel wait $7.5-6=1.5$ days before it’s reused

To decrease the waiting time (improve the utility), we could decrease the headway to $H=2$, so that the wating time is then zero.