Introduction to Trucking: Truckload, LTL, Package

• Truckload firms: Swift ($3.1) , Schneider National ($2.7), J.B. Hunt ($2.6), Landstar ($2.2), Prime ($1.9), Werner ($1.9)
• Less-than-truckload firms: Contract for shipments of pallets, boxes (150-10,000 lbs) FedEx Freight ($7.3), Old Dominion ($4.0), XPO ($3.8), YRC Freight ($3.2), Estes ($2.8), UPS Freight ($2.7)
• Package firms: Contract for smallest shipments such as flats, boxes (< 150 lbs) United Parcel Service ($69.3), FedEx ($57.7)

Note that smaller shipments = more network economies = fewer firms

Equipment types in fleets: Single-unit trucks, Tractor-semitrailer combination, Multi-trailer combinations

Network design and planning

• Physical facility location design
• Transportation freight flow design
• Load and dispatch planning
• Empty movement planning
• Operator scheduling

LTL Network Design

Multi-commodity Network Design

• $\sum_{(i,j)\in\delta^+(i)} x_{ij}^k - \sum_{(j,i)\in\delta^-(i)} x_{ji}^k = \begin{cases} +q_k &\text{if } i=o_k \ -q_k &\text{if } i=d_k \ 0 &\text{otherwise} \end{cases}$
• $\sum_k x_{ij}^k \leq y_{ij}$

where

• $h_i$: cost per trailerload of transfering freight at terminal $i$
• $y_{ij}$: integer number of trailers to dispatch on lane $y_{ij}$
• $x^k_{ij}$: commodity $k$ flow on arc $(i,j)$ (unit is in trailerloads)

Single-path Network Design: Let $x_{ij}^k=1$ indicates that lane $(i,j)$ is used for commodity $k$

• $\sum_{(i,j)\in\delta^+(i)} x_{ij}^k - \sum_{(j,i)\in\delta^-(i)} x_{ji}^k = \begin{cases} +1 &\text{if } i=o_k \ -1 &\text{if } i=d_k \ 0 &\text{otherwise} \end{cases}$
• $\sum_k q_k x_{ij}^k \leq y_{ij}$

如果还需要 balance empties: $\sum_{(i,j)\in\delta^+(i)} y_{ij} - \sum_{(j,i)\in\delta^-(i)} y_{ji} = 0$

Forcing an in-tree to each destination In-tree 指的是对于同一种商品, 在经过同一个点之后的路径相同。如下图：

• 左图的经过点不同, 所以路径可以不同: 是 in-tree
• 中间图的红蓝再经过同一个点之后的路径相同: 是 in-tree
• 右图的红蓝再经过同一个点之后的路径不同: 所以不是 in-tree

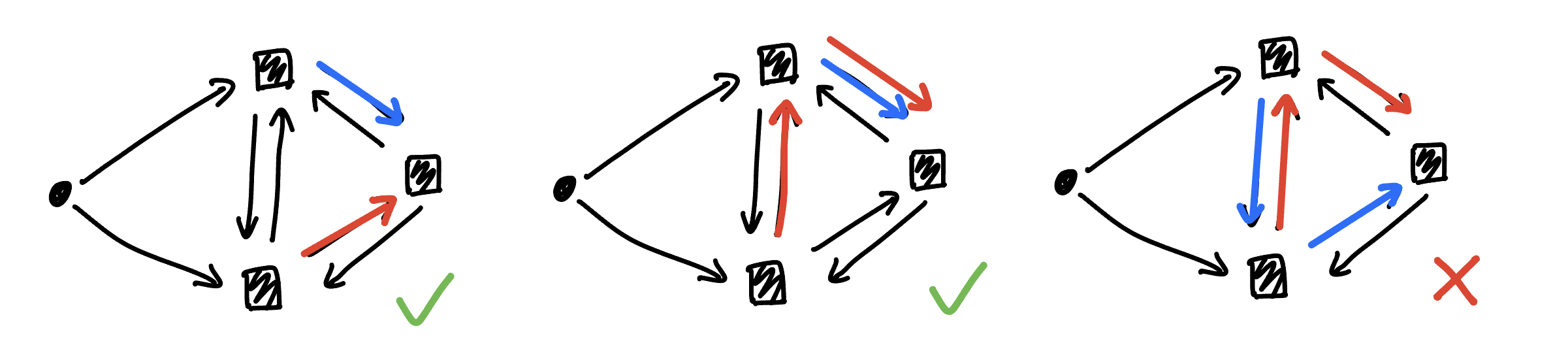
variables:

• $z_{ij}^d = 1$ if freight with dest $d$ at terminal $i$ must transfer next to $j$
• $\sum_{(i,j)\in\delta^+(i)} z_{ij}^d \leq 1$ for all $i,d$
• $x_{ij}^k \leq q_k z_{ij}^{d_k}$ for all $k,(i,j)$