Probability Distributions

1. PMF, PDF, CDF

Probability Mass Function (PMF)

Let $X$ be a random variable, and $x_1,…,x_M$ are possible outcomes

Then we define PMF as: \(p_X(x)=P(X=x)\)

And the probability of a certain range is: \(P(a< X\leq b)=F_X(b)-F_X(a)\)

Probability Density Function (PDF)

For continuous random variables, the probability at any single point is zero. That’s why we need PDF:

Cumulative Distribution Function (CDF)

For discrete r.v.: \(F(a)=P(X\leq a)=\sum_{x\leq a}p_X(x)\)

For continuous: \(F(a)=P(X\leq a)=\int_{-\infty}^af(x)dx\)

In addition, $p$ quantile is $\gamma$ such that \(Pr(X\leq\gamma)=F(\gamma)=p\)

2. Statistics Descriptor

Median: $x_{0.5}\to F(x_{0.5})=0.5$

Mode: $\tilde{x}\to \max f(x)=f(\tilde{x})$

Expectation (mean): $E[X]=\mu_X=\begin{cases}\sum_{\forall x}xp(x) \ \int_{-\infty}^\infty xf(x)dx\end{cases}$

Mean of Function: $E[g(X)]=\mu_X=\begin{cases}\sum_{\forall x}g(x)p(x) \ \int_{-\infty}^\infty g(x)f(x)dx\end{cases}$

Mean Square: $E[X^2]=\begin{cases}\sum_{\forall x}x^2p(x) \ \int_{-\infty}^\infty x^2f(x)dx\end{cases}$

Variance: \(Var(X)=E[(X-\mu_X)^2]=\begin{cases}\sum_{\forall x}(x-\mu_X)^2p(x) \\ \int_{-\infty}^\infty (x-\mu_X)^2f(x)dx\end{cases}\)

($Var(X)=E[X^2]-E[X]^2$)

Standard Deviation (std): $\sigma=\sqrt{Var(X)}$

Variance (c.o.v.): $\delta=\sigma/\mu$

Skewness Coefficient: $\gamma=\frac{E[(X-\mu_X)^3]}{\sigma^3}$

Relations

(1) $V[X]=E[X^2]-E^2[X]$

(2) $E[(X-\mu_X)^3]=E[X^3]-3E[X^2]E[X]+2E^3[X]$ Shape of $f(x)$ could be roughly known through: \(E[(x-\mu_X)^3]\begin{cases} \gt 0 & \text{means it has a tail to rightside}\\ =0 & \text{symmetric}\\ <0 & \text{a tail to leftside} \end{cases}\)

2.1 Calculation Rules

(1) $\begin{cases} E[aX]=aE[X]
E[X+b]=E[X]+b \end{cases}$

(2) $\begin{cases} Var(aX)=a^2Var(X)
Var(X)=Var(-X)
Var(X+b)=Var(X) \end{cases}$

(4) $V[X_1X_2]=E[X_1^2]E[X_2^2]-E^2[X_1]E^2[X_2]$

For Joint Distributions

2.2 Conditional Discripter

(1) $E[X\vert Y]=\int xf(x\vert y)dx$

(2) $V[X\vert Y]=\int (x-\mu_{x\vert y})^2f(x\vert y)dx$

(3) $E[X]=\int E[X\vert Y]f(y)dy$

2.3 Joint Case Descriptor

Expectation (mean):

$E[XY]=\begin{cases}\sum_x\sum_yxyp(x,y) \ \int\int xyf(x,y)dxdy\end{cases}$

Covariance: $Cov[X,Y]=\begin{cases}\sum_x\sum_y(x-\mu_X)(y-\mu_Y)p(x,y) \ \int\int(x-\mu_X)(y-\mu_Y)f(x,y)dxdy\end{cases}$

Relations $Cov[X,Y] = E[(X-\mu_X)(Y-\mu_Y)] = E[XY]-E[X]E[Y]$

Correlation Coefficient: \(\rho=\frac{Cov[X,Y]}{\sigma_X\sigma_Y}\)

(1) $-1\leq\rho\leq 1$ (2) $\rho=0$ uncorrelated (3) $\rho=-1,1$ perfect neg/pos correlated

S.I. vs Uncorrelated (1) S.I. must means uncorrelated. Since for S.I., $E[XY]=E[X]E[Y]$, then $Cov[X,Y]=0$ and $\rho=0$ (2) Uncorrelated may not means S.I.

2.3.1 Calculation Rules

(1) $Cov[X,X]=Var(X)=\sigma^2$

(2) $Cov[aX,bY]=ab\times Cov[X,Y]$

2.4 Sample Case

Sample Mean $\hat{\mu}_x=\bar x=\frac{1}{n}\sum x_i$

Sample Variace $\hat\sigma^2_x=s^2=\frac{1}{n-1}\sum(x_i-\bar x)^2$

Covariance $\hat{cov}(x,y)=\frac{1}{n}x_iy_i-\bar x\bar y$

3. Discrete Probability Function

3.1 Bernoulli Distribution

(Binary Distribution)

(1) $E[X]=p$

(2) $Var(X)=pq$

3.2 Binomial

\(P(Y=y)=f(y)=\begin{pmatrix}n \\ y\end{pmatrix}p^k(1-p)^{n-y}\)

$Y\sim\text{Binomial}(n,p)$ if it counts the number of successes in $n$ independent $\text{Bernouli}(p)$ trials. Alternatively, $Y=\sum_{i=1}^nX_i$, where $X_i\sim\text{Bernouli}(p)$

(1) $E[X]=np$

(2) $Var(X)=np(1-p)=npq$

(3) \(\delta=\frac{\sigma}{\mu} = \sqrt{\frac{1-p}{np}}\)

(4) $E[(x-\mu_X)^3]=np(2p^3-3p+1)$

(5) \(\gamma=\frac{E[(x-\mu_X)^3]}{\sigma^3}=\frac{1-2p}{\sqrt{np(1-p)}}\)

3.3 Poisson 泊松分布

当一个随机事件（来到某公共汽车站的乘客、显微镜下某区域内的白血球），以固定的速率 $\nu$（或称密度）随机且独立地出现时，那么这个事件在单位时间（面积）内出现的次数或个数就近似地服从泊松分布 $P(x)$

where $\nu>0, x=0,1,2,…$

(1) $\mu_X=\nu$

(2) $E[X^2]=\nu^2+\nu$

(3) $V[X]=E[X^2]-E^2[X]=\nu$

(4) $\sigma=\sqrt\nu$

(5) $\delta=\frac{1}{\sqrt\nu}$

示例：已知一个粒子平均每小时衰变5次，则其在3个小时内共衰变10次的概率为 $P(x=10)=\frac{(53)^{10}}{10!}\exp(-53)$

3.4 Exponential 指数分布

指数分布。表示独立随机事件发生的时间间隔的分布

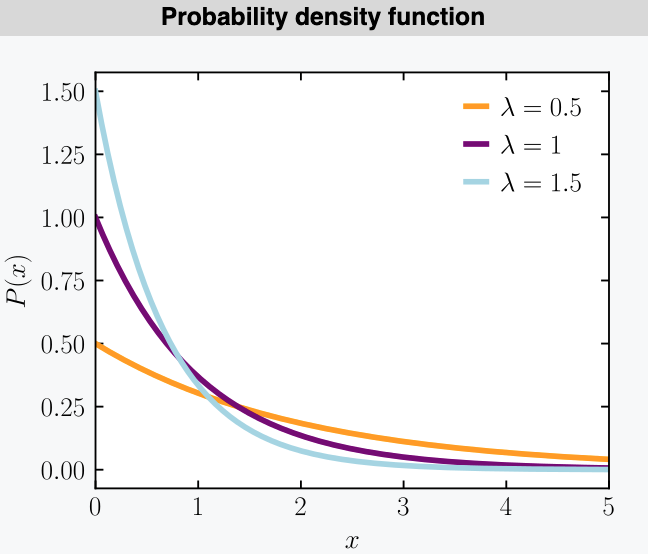
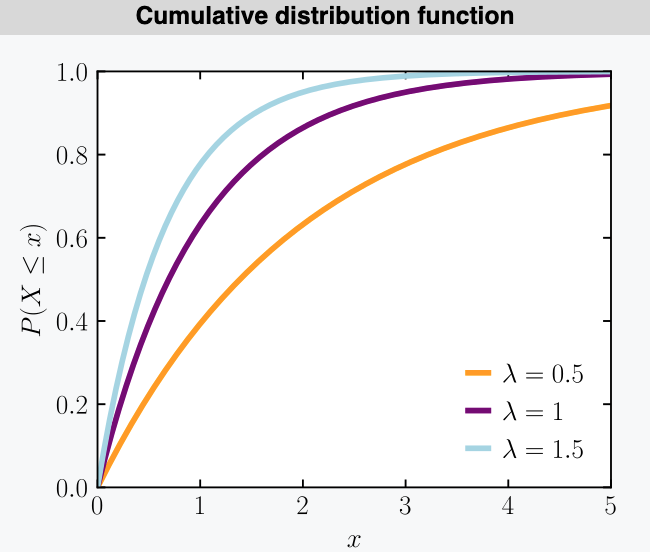
where $x\geq0, \lambda>0$

(1) $\mu_X=\frac{1}{\lambda}$

(2) $E[X^2]=\frac{2}{\lambda^2}$

(3) $V[X]=\frac{1}{\lambda^2}$

(4) $E[(x-\mu_X)^3]=\frac{2}{\lambda^3}$

(5) $\gamma=2$

Using part of exponential distribution, we could construct a new pdf function (unchecked): \(f(x)=cx^{k-1}\exp(-\lambda x)\)

where $k$ is the shape parameter, $c>0$

As a pdf, it should satisfy $\int_{-\infty}^\infty f(x)dx=1$

Here we define Gamma Function as $\Gamma(k)=\int_0^\infty u^{k-1}\exp(-u)du$, then $c=\frac{\lambda^k}{\Gamma(k)}$, so finally: \(f(x)=\frac{\lambda^k}{\Gamma(k)}x^{k-1}\exp(-\lambda x)\)

Properties of $\Gamma(k)$ (1) $\Gamma(k) = (k-1)!$ (2) $\Gamma(k+1) = k\Gamma(k)$ (3) $\Gamma(\frac{1}{2})=\pi$

3.5 Gamma

Gamma 分布等同于多个独立且相同分布（idd）的指数分布变量的和的分布

Same as the equation mentioned right above

Process of getting CDF \(\begin{split} F(x) &=\int_0^x \frac{\lambda(\lambda z)^{k-1}}{\Gamma(k)}\exp(-\lambda z)dz \\ & \text{let }u=\lambda z, dz=\frac{1}{\lambda}du,\text{ then}\\ &= \int_0^{\lambda x} \frac{u^{k-1}}{\Gamma(k)}\exp(-u)du \\ &= \frac{1}{\Gamma(k)}\int_0^{\lambda x} u^{k-1}\exp(-u)du \\ &= \frac{\Gamma(k, \lambda x)}{\Gamma(k)} \end{split}\)

(1) $E[X^m]=\frac{\Gamma(k+m)}{\lambda^m\Gamma(k)}=\frac{(k+m-1)(k+m-2)…k}{\lambda^m}$

Process \(\begin{split} E[X^m] &= \frac{\Gamma(k+m)}{\Gamma(k+m)}\frac{\lambda^m}{\lambda^m}\int_0^\infty x^m\frac{\lambda(\lambda x)^{k-1}}{\Gamma(k)}\exp(-\lambda x)dx \\ &= \frac{\Gamma(k+m)}{\lambda^m\Gamma(k)} \int_0^\infty \frac{\lambda(\lambda x)^{k+m-1}}{\Gamma(k+m)}\exp(-\lambda x)dx \\ &= \frac{\Gamma(k+m)}{\lambda^m\Gamma(k)} \end{split}\)

(2) $E[X]=\frac{k}{\lambda}$, $E[X^2]=\frac{k(k+1)}{\lambda^2}$, $E[X^3]=\frac{k(k+1)(k+2)}{\lambda^3}$

(3) $V[X]=\frac{k}{\lambda^2}, \delta=\frac{1}{\sqrt{k}}, \gamma=\frac{2}{\sqrt k}$

(4) When $k=1$, $f(x)=\lambda\exp(-\lambda x)$, exponential distribution!

3.6 Geometric

aka. gmetric distribution, 几何分布

(1) $E[X]=1/p$

(2) $Var(X)=(1-p)/p^2$

4. Continuous Probability Functions

4.1 Uniform Distribution

\(f(x)=\frac{1}{b-a}\quad F(x)=\frac{x-a}{b-a}\)

where $a\leq x\leq b$

(1) $E[X^m] = \int_{a}^b \frac{x^m}{b-a}dx = \frac{b^{m+1}-a^{m+1}}{(m+1)(b-a)}$

(2) $E[X]=\frac{b+a}{2}$, $E[X^2]=\frac{b^2+ab+a^2}{3}$$

(3) $V[X]=\frac{(b-a)^2}{12}$, $\sigma=\frac{b-a}{2\sqrt 3}$

(4) $E[(X-\mu_X)^3]=0$, because of symmetric (see Section 7.1)

(5) Standard Uniform Distribution: $b=1, a=0$

4.2 Normal

$X\sim N(\mu, \sigma^2)$ \(f(x)=\frac{1}{\sqrt{2\pi}\sigma}\exp[-\frac{1}{2}(\frac{x-\mu}{\sigma})^2]\)

(1) $E[(X-\mu)^m]=0$ for odd $m$, $\frac{m!\sigma^m}{(m/2)!2^{m/2}}$ for even $m$

4.2.1 Standard Normal Distribution

Denoted as $U$ or $N(0,1)$ \(f_U(u)=\phi(u)=\frac{1}{\sqrt{2\pi}}\exp(-\frac{1}{2}u^2)\)

Obviously, $\Phi(-u)=1-\Phi(u)$

4.2.2 Lognormal Distribution

$LN(\lambda, \xi)$: \(f(x)=\frac{1}{\sqrt{2\pi}\xi x}\exp[-\frac{1}{2}(\frac{\ln x-\lambda}{\xi})^2]\)

where $x>0$

(1) $\mu=\exp(\lambda+\frac{1}{2}\xi^2)$

(2) $\delta=\frac{\sigma}{\mu}=\sqrt{\exp(\xi^2)-1}$

(3) $\xi=\sqrt{\ln(1+\delta^2)}$

(4) $\lambda=\ln\mu-\frac{1}{2}\xi^2$

(5) $\xi\approx\delta$, when $\delta^2$ is very small

5. Multinormal Distribution

\(f(\bf{x})=(2\pi)^{-\frac{n}{2}}\vert\bf\Sigma\vert^{-\frac{1}{2}} \exp\Big[-\frac{1}{2}(\bf{x}-\bf{\mu})^T\vert\bf\Sigma\vert^{-1}(\bf{x}-\bf{\mu})\Big]\)

where

1. $\bf{x-\mu}=[x_1-\mu_1,…,x_n-\mu_n]^T$
2. $\bf\Sigma=\begin{bmatrix} \sigma_1^2 & 0 & … & 0
   0 & \sigma_2^2 & … & 0
   … & … & … & ….
   0 & … & 0 & \sigma_n^2 \end{bmatrix}$

14.1 (m=1) (Univariate) Normal Distribution

\(f(x)=\frac{1}{\sqrt{2\pi}\sigma}\exp\Big[-\frac{1}{2}(x-\mu)\sigma^{-2}(x-\mu)\Big]\)

14.2 (m=2) Bi-variate Normal Distribution

\(f(x_1,x_2)=\frac{1}{2\pi\sigma_1\sigma_2\sqrt{1-\rho^2}}\exp\Big\{-\frac{1}{2(1-\rho^2)}\Big[(\frac{x_1-\mu_1}{\sigma_1})^2-2\rho(\frac{x_1-\mu_1}{\sigma_1})(\frac{x_2-\mu_2}{\sigma_2})-(\frac{x_2-\mu_2}{\sigma_2})^2\Big]\Big\}\)