2021.03.07 Updates
Reference 1.B站:机器学习-白板推导系列(二十)-高斯过程GP(Gaussian Process) 2.CSDN:一文搞定(二)—— 贝叶斯线性回归 3.知乎:Gaussian process regression的导出——权重空间视角下的贝叶斯的方法 4.知乎:高斯过程 Gaussian Processes 原理、可视化及代码实现
Contents 1 Introduction 简要介绍 2 Weigh-space view GPR 的权重空间角度 3 Fron wsv to fsv 从权重空间到函数空间是如何过渡的 4 Function-space view GPR 的函数空间角度 5 Example in code 包含对于一个简单 GPR 示例的 python 和 matlab 两种语言的代码
Reading Tip 对于希望直接应用的读者可以跳过 Section 2, 3 两部分,直接看 Section 1, 4, 5
1. Introduction: 从高斯分布到高斯过程
1.1 多元高斯分布
\[\tag{1} p(\bf{x})=\prod_{i=1}^n p(x_i)=\frac{1}{(2\pi)^{\frac{n}{2}}\sigma_1...\sigma_n}\exp(-\frac{1}{2}[\frac{(x_1-\mu_1)^2}{\sigma_1^2}...\frac{(x_n-\mu_n)^2}{\sigma_2^2}])\]进一步的,令:
- $\bf{x-\mu}=[x_1-\mu_1,…,x_n-\mu_n]^T$
- $\bf\Sigma=\begin{bmatrix} \sigma_1^2 & 0 & … & 0 \newline 0 & \sigma_2^2 & … & 0 \newline … & … & … & …. \newline 0 & … & 0 & \sigma_n^2 \end{bmatrix}$
从而可得多元高斯分布的向量化表示:
\[\tag{2} p(\bf{x})=(2\pi)^{-\frac{n}{2}}\vert \bf\Sigma\vert ^{-\frac{1}{2}}\exp(-\frac{1}{2}(\bf{x}-\bf{\mu})^T\vert \bf\Sigma\vert ^{-1}(\bf{x}-\bf{\mu}) )\](留意上式中的 $(\bf{x}-\bf{\mu})^T\vert \bf\Sigma\vert ^{-1}(\bf{x}-\bf{\mu})$,它与下文将要介绍的 kernel function 有着类似的形式)
1.2 高斯过程 Gaussain Process
高斯过程是定义在连续域上的无限多个高维随机变量所组成的随机过程,可以看做是一个无限维的高斯分布。在作者的理解中,通过高斯过程,我们能够将离散的点分布转化为函数的分布。(当然,这些离散点本身需要满足高斯分布)
借用参考资料 4 中的插图,高斯过程在下图中的体现就是将红色的离散点变成蓝色的函数曲线 (该曲线不仅能够储存原离散数据集的部分特征,还能用于预测): 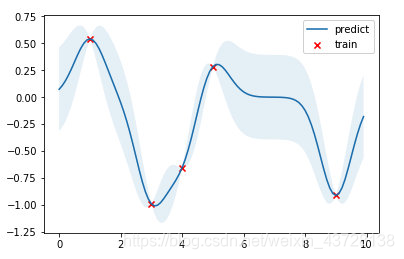
GP 的数学定义
对于随机变量 ${\zeta_t}{t\in T}$ ($T$ 可以是连续的时间或空间),如果对于任意 $n\in \N^+,\;\;t_1,…,t_n\to \zeta_1,…,\zeta_n$, 都有 $\bf{\zeta}=(\zeta_1,…,\zeta_n)^T \sim N(\bf{\mu},\bf{\Sigma})$, 那么 ${\zeta_t}{t\in T}$ 就是一个高斯过程,记做
\[\tag{3}\zeta_t\sim GP(m(t),\kappa(s,t))\]- $m(t)=E[\zeta_t]$, mean function
- $\kappa(t,s)=E[(\zeta_s-m(s))(\zeta_t-m(t))^T]$, covariance function
1.3 高斯过程回归 Gaussian Process Regression
- weight-space view: 关注的是 $w$
- function-space view: 关注的是 $f(x)$
2. Weight-space view
回顾贝叶斯线性回归(见参考资料 2)
(1) Inference: 求后验 $P(w\vert Data)=N(w\vert \mu_w,\Sigma_w)$
- $\mu_w=\sigma^{-2}A^{-1}X^TY$
- $\Sigma_w=A^{-1}$
- $A=\sigma^{-2}X^TX+\Sigma_P^{-1}$
(2) Prediction: $\text{Given }x^*$
- $P(f(x^)\vert Data,x^)=N((x^)^T\mu_w,(x^)^T\Sigma_wx^*)$
- $P(y^\vert Data,x^)=N((x^)^T\mu_w,(x^)^T\Sigma_wx^*+\sigma^2)$
但如果遇到的模型是非线性的,一般的做法可以是先做一个非线性转换 $z=\phi(x),\;\;x\in\R^p,\;\;z\in\R^q$,然后再使用贝叶斯线性回归(该非线性转换一般把数据由低维转换成高维)
2.1 Process
考虑不存在噪音的情况:
\[f(x^*)\vert X,Y,x^*\sim N(x^*(\sigma^{-2}A^{-1}X^TY),(x^*)^TA^{-1}x^*)\]where, $A=\sigma^{-2}X^TX+\Sigma_P^{-1}$
If $\phi:x\mapsto z,\;\;x\in\R^p,\;\;z=\phi(x)\in\R^q,\;\;q>p$
Define
- $\Phi=\phi(X)=[(\phi(x_1),…,\phi(x_N))^T]_{N\times q}$
- $X=[(x_1,…,x_N)^T]_{N\times p}$
- $Y=(y_1,…,y_N)^T$
then $f(x)=\phi(x)^Tw$, let $\phi_$ denotes $\phi(x^)$, finally we have
\[f(x^*)\vert X,Y,x^*\sim N(\phi_*(\sigma^{-2}A^{-1}\Phi^TY),\phi_*^TA^{-1}\phi_*)\]where, $A=\sigma^{-2}\Phi^T\Phi+\Sigma_P^{-1}$
如何计算 $A^{-1}$? 使用:Woodbury formula
\[(A+UCV)^{-1}=A^{-1}-A^{-1}U(C^{-1}+VA^{-1}U)^{-1}VA^{-1}\]由此可得, (1) mean: $\phi_(\sigma^{-2}A^{-1}\Phi^TY)=\phi_\Sigma_p\Phi^T(K+\sigma^2I)^{-1}Y$ (2) covariance: $\phi_{}^TA^{-1}\phi_{} = \phi_{}^T\Sigma_p\phi_{} - \phi_{}^T\Sigma_p\Phi^T(K+\sigma^2I)^{-1}\Phi\Sigma_p\phi_{}$ where, $K=\Phi^T\Sigma_p\Phi$
2.2 kernel funciton 的意义
观察 $\kappa(x,x’)$
\[\begin{aligned} \kappa(x,x') &= \phi(x)^T\Sigma_p\phi(x')=\phi(x)^T\Sigma_p^{\frac{1}{2}}\Sigma_p^{\frac{1}{2}}\phi(x') \newline &= (\Sigma_p^{\frac{1}{2}}\phi(x))^T(\Sigma_p^{\frac{1}{2}}\phi(x')) \newline &=<\psi(x),\psi(x')> \end{aligned}\]可见它可以被简化成两数内积的形式。若进一步观察均值和协方差的表达式,我们观察到除了 $Y$ 以及 $\sigma^2I$,其余的所有部分都可以用 kernel function $\kappa(x,x’)$ 来表达
由于该kernel已经包含了原特征空间的所有信息,从而能够成为原先方法的一种简单替代。
GP过程中kernel function的重要性就在于它能将一个复杂问题转化成只需要考虑kernel的简单问题。
2.3 总结
weight-space view of GPR = Bayesian Linear Regression + Kernel trick (Non-linear Transformation, innner product)
3. From wsv to fsv
先回顾对高斯过程的定义
对于随机变量 ${\zeta_t}_{t\in T},\;\;T:\text{continuous time/ space}$
如果对于任意 $\;\forall\; n\in \N^+$, 都存在映射 $t_1,…,t_n\to \zeta_1,…,\zeta_n$ such that $\bf{\zeta}=(\zeta_1,…,\zeta_n)^T \sim N(\bf{\mu},\bf{\Sigma})$, 那么就把 ${\zeta_t}_{t\in T}$ 记为高斯过程, 即
\[\zeta_t\sim GP(m(t),\kappa(t,s))\]再回顾 weight-space view(其关注的对象为 $w$)
$\begin{cases} f(x)=\phi(x)^Tw
y=f(x)+\varepsilon,\;\;\varepsilon\sim N(0,\sigma) \end{cases}$
结合 Section 2.3 中的结论,可以发现 GPR 的 wsv 和 GP 的定义似乎没啥关系。
的确如此,wsv 本质上是贝叶斯线性推断和核方法的结合物,只是能够恰好从另一方面体现高斯过程。而 function-space view 关注的对象则是 $y$,正如 GP 所定义的那样
就具体问题而言,使用 wsv 还是 fsv 没有差别
4. Function-space view
假设样本集 ${f(x)}$ 满足
\[\{f(x)\}_{x\in \R^p}\sim GP(m(x),\kappa(x,x'))\]where,
- $m(x)=E[f(x)]$
- $\kappa(x,x’)=E[(f(x)-m(x))(f(x’)-m(x’))^T]$
4.1 Regression
$\text{Data}:{(x_i,y_i)}_{i=1}^N,\;y=f(x)+\varepsilon$
$X=[(x_1,…,x_N)^T]{N\times p}\;\;\;\; Y=[(y_1,…,y_N)^T]{N\times 1}$
\[f(X)\sim N(\mu(X),\kappa(X,X)) \\ Y=f(X)+\varepsilon \sim N(\mu(X),\kappa(X,X)+\sigma ^2I)\]4.2 Prediiction
$\text{Given}\;X^=(x_1^,…,x_M^)^T, \text{calculate}\;Y^=f(X^*)+\varepsilon$
\[\begin{pmatrix} Y \\ f(X^*) \end{pmatrix} \sim N\begin{pmatrix} \begin{pmatrix} \mu(X) \\ \mu(X^*) \end{pmatrix}, \begin{pmatrix} \kappa(X,X)+\sigma^2I & \kappa(X,X^*) \\ \kappa(X^*,X) & \kappa(X^*,X^*) \end{pmatrix} \end{pmatrix}\]已知公式,对于 $X\sim N(\mu,\Sigma)$ \(\text{If}\;X=\begin{pmatrix} X_a \\ X_b \end{pmatrix}, \mu=\begin{pmatrix} \mu_a \\ \mu_b \end{pmatrix}, \Sigma=\begin{pmatrix} \Sigma_{aa} & \Sigma_{ab} \\ \Sigma_{ba} & \Sigma_{bb} \end{pmatrix} \\ \text{then we have }X_b\vert X_a\sim N(\mu_{b\vert a},\Sigma_{b\vert a})\)
where,
- $\mu_{b\vert a}=\Sigma_{ba}\Sigma_{aa}^{-1}(X_a-\mu_a)+\mu_b$
- $\Sigma_{b\vert a}=\Sigma_{bb}-\Sigma_{ba}\Sigma_{aa}^{-1}\Sigma_{ab}$
根据该公式可得
\[P(f(X^*)\vert Y,X,X^*)=P(f(X^*)\vert Y)\sim N(\mu^*,\Sigma^*)\]where,
- $\mu^=\kappa(X^,X)(\kappa(X,X)+\sigma^2I)^{-1}(Y-\mu(X))+\mu(X^*)$
- $\Sigma^=\kappa(X^,X^)-\kappa(X^,X)(\kappa(X,X)+\sigma^2I)^{-1}\kappa(X,X^*)$
因此,
\[P(y^*\vert Y,X,X^*)\sim N(\mu^*,\Sigma^*+\sigma^2I)\]5. Example in code
简单高斯过程回归实现 (斜体部分内容来自参考资料 4)
考虑代码实现一个高斯过程回归,API 接口风格采用 sciki-learn fit-predict 风格。由于高斯过程回归是一种非参数化 (non-parametric) 的模型,每次的 inference 都需要利用所有的训练数据进行计算得到结果,因此并没有一个显式的训练模型参数的过程,所以 fit 方法只需要将训练数据保存下来,实际的 inference 在 predict 方法中进行。
结果如下图,红点是训练数据,蓝线是预测值,浅蓝色区域是 95% 置信区间。真实的函数是一个 cosine 函数,可以看到在训练数据点较为密集的地方,模型预测的不确定性较低,而在训练数据点比较稀疏的区域,模型预测不确定性较高。 
python 实现
详见 参考资料 4
matlab 实现
定义类
classdef GPR
properties
is_fit = 0;
train_X = nan;
train_y = nan;
params = struct('l', 0.5, 'sigma_f', 0.2);
end
methods
function obj = GPR()
end
function obj = fit(obj, X, y)
obj.train_X = X;
obj.train_y = y;
obj.is_fit = 1;
end
function [mu, cov] = predict(obj, X)
if obj.is_fit == 0
disp('model not fit yet')
end
Kff = obj.kernel(obj.train_X, obj.train_X);
Kyy = obj.kernel(X, X);
Kfy = obj.kernel(obj.train_X, X);
Kff_inv = inv(Kff + 1e-8 * eye(length(obj.train_X)));
mu = Kfy' * Kff_inv * obj.train_y;
cov = Kyy - Kfy' * Kff_inv * Kfy;
end
function result = kernel(obj, x1, x2)
distance = x1.^2 + (x2.^2)' - 2 * x1 * x2';
sigma_f = obj.params.('sigma_f');
l = obj.params.('l');
result = sigma_f^2 * exp(-distance/(2*l^2));
end
end
end
训练 + 预测
train_X = [3, 1, 4, 5, 9]';
train_y = cos(train_X);
test_X = 0:0.1:10;
test_X = test_X';
gpr = GPR();
gpr = gpr.fit(train_X, train_y);
[mu, cov] = gpr.predict(test_X);
uncertainty = 1.96 * sqrt(diag(cov));
figure;
xfill = [test_X', fliplr(test_X')];
yfill = [(mu - uncertainty)', fliplr((mu + uncertainty)')];
fill(xfill, yfill, 'c', 'FaceAlpha', 0.5, 'EdgeAlpha', 1, 'EdgeColor', 'c');
hold on;
plot(test_X, mu);
结果示意图 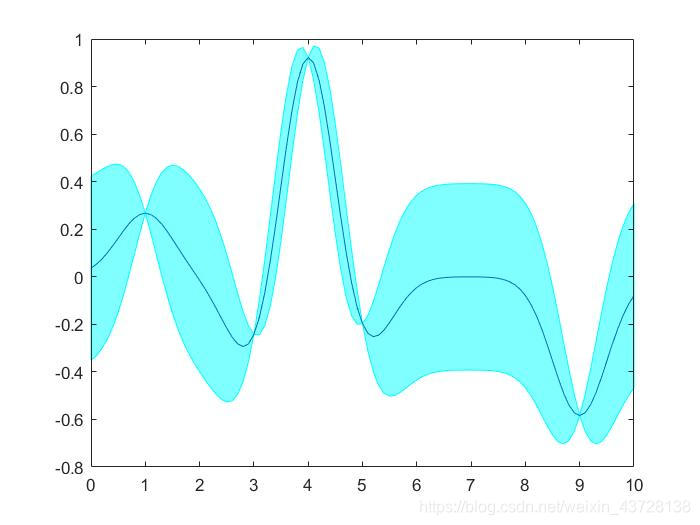
Document Information
- Author: Zeka Lee
- Link: https://zhekaili.github.io/0008/03/01/Gaussian-Process-Regression/
- Copyright: 自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)