# Graph and Network Basic

使用 Java 实现，Github 代码仓：https://github.com/ZhekaiLi/Code/tree/main/Graph/src

1. Classifications

1.1 Undirected vs Directed

无向图(undirected graph) $G$ 是由一个非空有限集合$V(G)$ 和 $V(G)$ 中某些元素的无序对集合 $E(G)$ 构成的二元组，记为 $G = (V (G),E(G))$

where,
$V(G)={v_1,v_2,…,v_n}$ 称为顶点集(vertex set)
$E(G)={e_1,e_2,…,e_n}$ 称为边集(edge set), $e_k=(v_i,v_j)$

如果一个图的顶点集和边集都有限，则称为有限图。使用符号 $\vert V\vert$ or $v(G)$ 表示顶点数，$\vert E\vert$ or $\varepsilon(G)$ 表示边数

有向图(directed graph 或 digraph) $G$ 是由一个非空有限集合 $V$ 和 $V$ 中某些元素的有序对集合 $A$ 构成的二元组，记为 $G = (V, A)$

where,
$A = {a_1, a_2, …, a_m}$ 称为弧集(arc set)。对于 $a_k = (v_i ,v_j)$，称 $v_i$ 为尾(tail), $v_j$ 为头(head)，并称弧 $a_k$ 为 $v_i$ 的出弧(outgoing arc)，为 $v_j$ 的 入弧(incoming arc)。

以下若未指明“有向图”三字，“图”字皆指无向图。

1.2 完全图、二分图

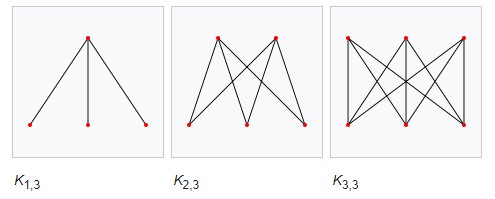
每一对不同的顶点都有一条边相连的简单图称为完全图(complete graph)。$n$ 个顶点的完全图记为 $K_n$。

若 $V(G) = X\cup Y, X\cap Y = \text{\O}, \vert X\vert\vert Y\vert\neq 0$，$X,Y$ 中无相邻顶点对，则称 $G$ 为二分图(bipartite graph)；特别地，若 $\forall x\in X, \forall y\in Y$，则 $xy\in E(G)$，则称 $G$ 为完全二分图，记为 $K_{\vert X\vert,\vert Y\vert}$。

示例：完全二分图

2. Basic Concepts

简单图

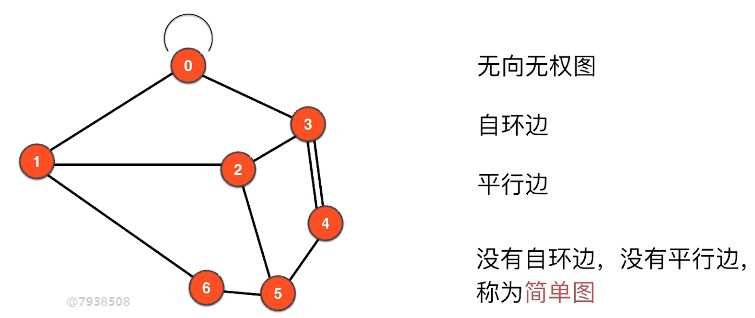
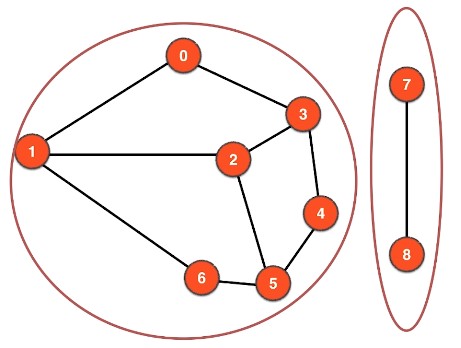
连通分量(Connected Component) 为一个图的极大连通子图，例如下图的连通分量为 2

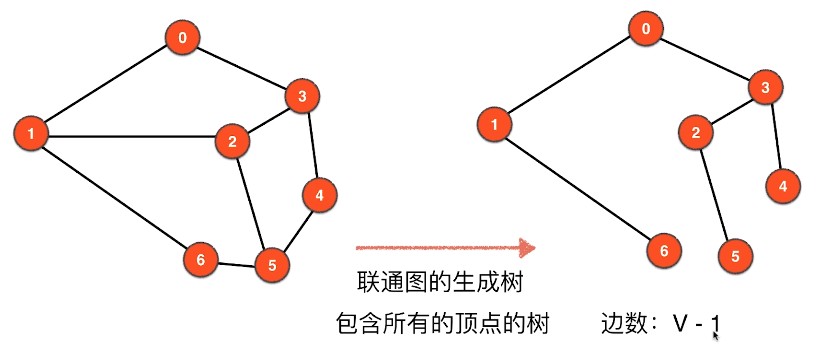
图的生成树

顶点的度

设 $v\subset V(G)$，$G$ 中与 $v$ 关联的边数(每个环算作两条边)称为 $v$ 的度(degree)，记作 $d(v)$。若 $d(v)$ 是奇数，称 $v$ 是奇顶点(odd point)，反之偶顶点(even point)。

子图、母图

如果 $V(H)\subset V(G), E(H)\subset E(G)$，则称 $H$ 为图 $G$ 的子图(subgraph)，记作 $H\subset G$。同时称 $G$ 为 $H$ 的母图。

$G$ 的支撑子图(spanning subgraph，又成生成子图)是指满足 $V(H) = V(G)$ 的子图 $H$。

3. Representations of Graph

用来描述图与网络的 5 种常用表示方法：邻接矩阵表示法、关联矩阵表示法、弧表表示法、邻接表表示法和星形表示法。

在下面数据结构的讨论中，首先假设 $G = (V, A)$ 是一个简单有向图，$\vert V\vert=n,\vert A\vert= m$，并假设 $V$ 中的顶点用自然数 $1,2,…,n$ 表示或编号，$A$ 中的弧用自然数 $1,2,…,n$ 表示或编号。

可以使用权重替换邻接矩阵、关联矩阵中的 $1,-1$，这两种表示方法都会由于网络的稀疏而浪费大量的存储空间

3.1 邻接矩阵

图 $G = (V, E)$ 的 邻接矩阵(adjacency matrix) $C$ 是如下定义的： $\begin{aligned} C&=(c_{ij})_{n\times n}\in\{0,1\}^{n\times n}\\ c_{ij}&=\begin{cases} 1,\;\;(i,j)\in E\\ 0,\;\;(i,j)\notin E \end{cases} \end{aligned}$

示例：有向图及其邻接矩阵

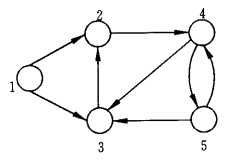
而对于无向图来说，其邻接矩阵是对称的（$c_{ij}=c_{ji}$）

可以用下图中央这样的两列数据来表示一个无向图，然后将其翻译为邻接矩阵

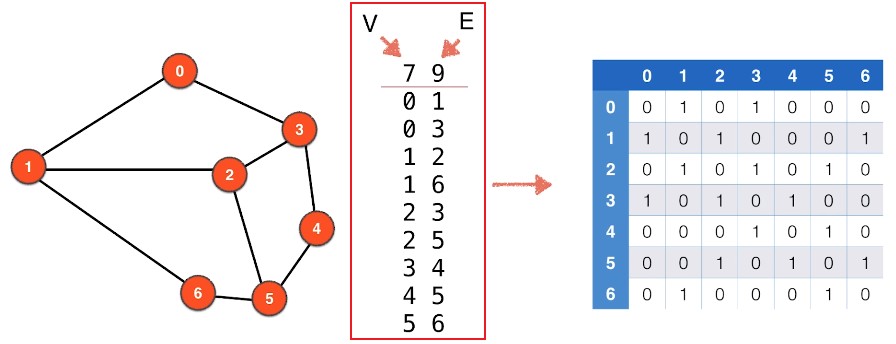
java 实现：AdjMatrix.java

3.2 邻接表

为什么要引入邻接表?（邻接矩阵的复杂度）

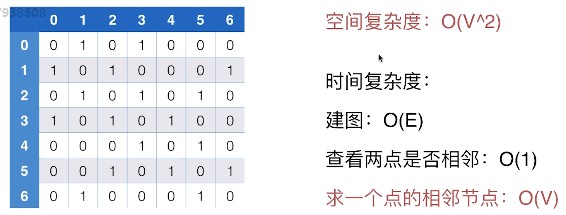
邻接矩阵的的建图时间复杂度 $O(E)$（遍历每条边），以及判断两点是否相邻的时间复杂度 $O(1)$ 没有提升空间，但其空间复杂度以及求相邻节点的时间复杂度较大

尤其是例如对于一个有3000个节点的树（无向图），它只有2999条边，即使是乘2也只有6000不到组数据，但是其对应的邻接矩阵的空间复杂度却是 $O(3000^2)$，近千倍的差距！

邻接表的定义

图的邻接表(adjacency list) 是所有节点的邻接表的集合各节点的邻接表由其：

邻边（无向图）
出弧（有向图）

组成，并用一个单向链表列出，链表中每个单元对应于一条邻边/出弧，此外还可以包含弧上的权等作为数据域。

邻接表的表示

对于有向图 $G = (V, E)$，一般用 $A(i)$ 表示节点 $i$ 的邻接表，即节点 $i$ 的所有出弧构成的集合或链表

对于无向图，$A(i)$ 则表示节点 $i$ 邻边的集合

图的整个邻接表还可以用一个指针数组表示。例如：（下图中第一个指针数组表示，$1\to2$ 的权重为8，$1\to3$ 的权重为9）

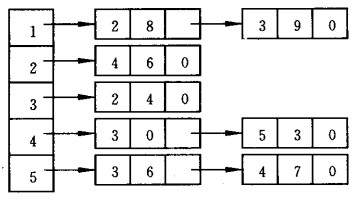
java 实现：AdjList.java

邻接表的复杂度

相较于邻接矩阵的复杂度，邻接表在空间复杂度、求相邻节点的时间复杂度这两方面有明显优势，但其建图的时间复杂度、判断两点是否相邻的时间复杂度较大。

降低这两个复杂度的关键在于实现快速查看重复边/ 快速判断两点是否相邻，因此我们可以使用哈希表 $O(1)$ 或红黑树 $O(\log V)$ 代替链表（在 java 中分别对应 HashSet, TreeSet, LinkedList）

java 实现：Graph.java（使用红黑树）

3.3 比较：矩阵 vs 两种表

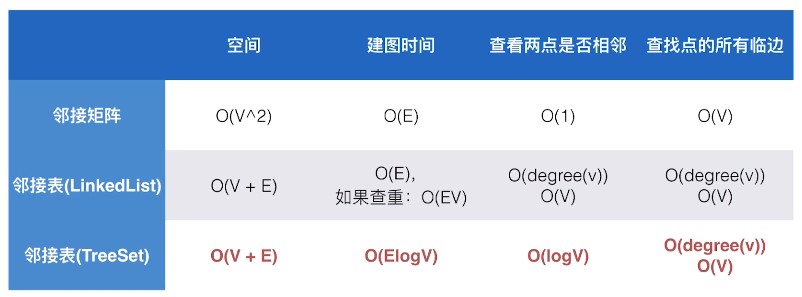
因此我门最终选用邻接表(TreeSet) 作为图的表达形式（当然也可以使用HashSet）

4. DFS (Deep-first Search)

（关于树的前、中、后、层序遍历，有一篇博客总结的挺好：https://blog.csdn.net/zl6481033/article/details/81009388）先来看树的深度优先遍历（以前序遍历为例）

preorder(root); // 从根结点开始遍历

preorder(TreeNode node)
    if(node != null)
        list.add(node.val);
        preorder(node.left);
        preorder(node.right);

图的深度优先先序遍历：与树略有不同的是，图算法在递归之前需要先判断节点是否被访问过，其时间复杂度为 $O(V+E)$

visited[0...V-1] = false;

// 使用 for 循环保证遍历每个点，使得算法可以应对非联通图
for(int v = 0; v < V; v++)
    if(!visited[v])
        dfs(v);

dfs(int v)
    visited[v] = true; // 标记为已访问
    list.add(v);
    for(int w: adj(v))
        if(!visited[w])
            dfs(w);

java 实现：GraphDFS.java

4.1 Ex: 求联通分量

也就是求解包含几张联通图

visited[0...V-1] = -1;
ccount = 0; // 联通分量

for(v = 0; v < V; v++)
    if(visited[v] == -1)
        dfs(v, ccount);
        ccount++;

dfs(v, ccid)
    visited[v] = ccid;
    list.add(v);
    for(int w: adj(v))
        if(visited[w] == -1)
            dfs(w, ccid);

java 实现：CC.java

求两点间是否可达：只需要如下判断即可

visited[v] == visited[w];

4.2 Ex: 求两点间路径

（不一定是最短）

// pre[i] = j 表示存在路径 j->i
// pre[i] = -1 表示尚未访问，代替 visited[i] = false
pre[0...V-1] = -1;
s = 0; // 自定义的起始点
t = 5; // 自定义的终止点

pre[s] = s; // 将源头的源头设为自己
dfs(s);

// 返回值表示是否达到了目标点 t
boolean dfs(int v)
    for(int w: adj(v))
        if(visited[w] == -1)
            pre[w] = v;
            if(w == t) return true;
            if(dfs(w)) return true;
    return false;

java 实现：Path.java

4.3 Ex: 环检测

java 实现：CycleDetection.java

4.4 Ex: 二分图检测

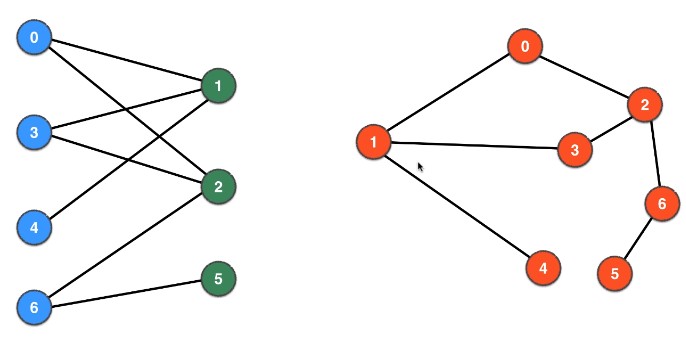
左右两个看起来完全不同的图其实是一样的，但是左侧的形式很显然是个二分图，而右侧更加普通、随机的形式却没办法直观地进行判断。

利用DFS进行二分图检测：

// -1: 未访问
// 0: 二分图的一侧
// 1: 二分图的另一侧
color[0...V-1] = -1;

color[0] = 0;
dfs(0);

// 返回值表示是否检测到了目标图不是二分图的证据
boolean dfs(int v)
    for(int w: adj(v))
        if(color[w] == -1)
            color[w] = 1 - color[v]
            if(dfs(w)) return true;
        else if(color[w] == color[v])
            return true
    return false;

java 实现：BipartitionDetection.java

5. BFS (Breath-first Search)

先来看树的广度优先遍历，下图展示了利用队列来进行树的BFS的大致过程

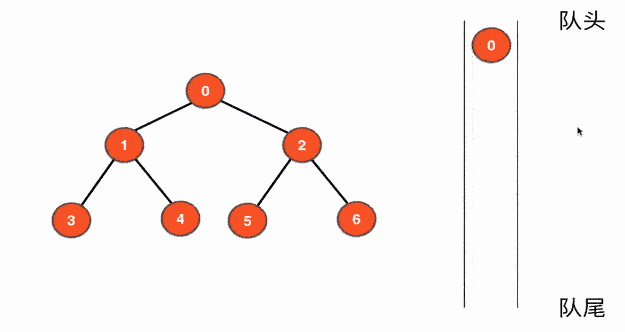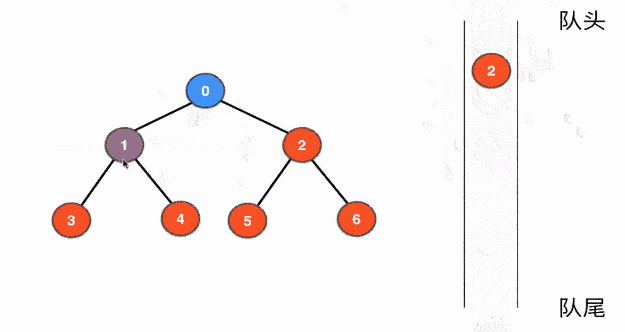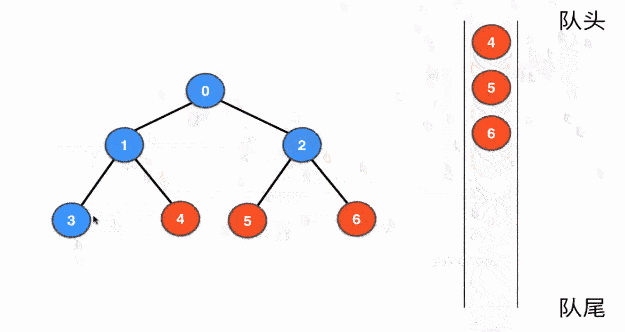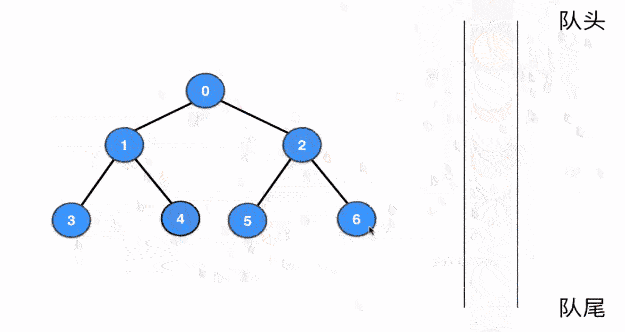
bfs(root); // 从根结点开始遍历

bfs(TreeNode node)
    queue.add(node);
    while(!queue.isEmpty)
        v = queue.remove();
        list.add(v);
        for(w: v.son())
            queue.add(w)

图的广度优先遍历在代码逻辑上与树的BFS相同，只是需要在 queue.add(w) 前添加一个结点 w 是否已经被访问的判断。时间复杂度同样为 $O(V+E)$

java 实现：GraphBFS.java

绝大部分DFS可以解决的问题同样可以由BFS解决

5.1 Ex: 求两点间路径

同理 Section 4.2

pre[0...V-1] = -1;
s = 0; // 自定义的起始点
t = 5; // 自定义的终止点

bfs(s); // 从根结点开始遍历

bfs(int v)
    queue.add(v);
    pre[v] = v;
    while(!queue.isEmpty)
        v = queue.pop();
        list.add(v);
        for(w: v.son())
            queue.add(w);
            pre[w] = v;

java 实现：SingleSourcePathBFS.java

5.2 性质：无权图最短路径

同样是从 $0\to6$，BFS的路径短于DFS，该性质同样适用于任意点，即BFS能够找到任意点与根节点间的最短路径

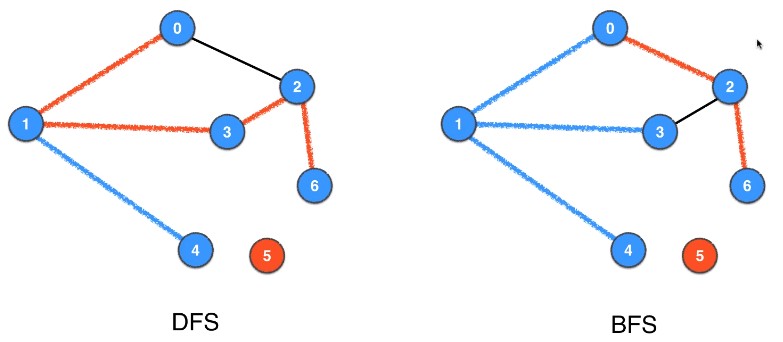
这是因为BFS是层序遍历，从根节点开始从近至远依次遍历，每次遍历寻找的都是最近的结点（可以理解为一种贪心算法，当边不含权重时，贪心 = 最优）

如果在遍历的过程中直接记录距离信息 dis[]，则可以直接读出根节点至任意结点的最短距离

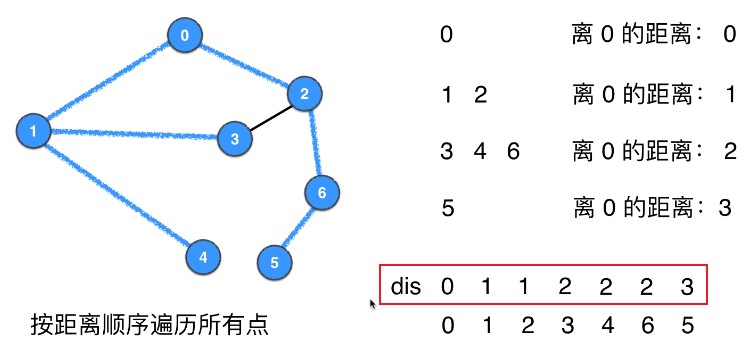
java 实现：USSSPath.java

5.3 比较：DFS vs. BFS

比较 BFS 与 DFS（非递归），我们发现唯一的不同在于 DFS 使用栈而 BFS 使用队列（处理结点时 DFS 头进头出，BFS 尾进头出）（statck.add(s)对应stack.push()，statck.remove()对应stack.pop()）

更进一步的，我们还可以用任意的结构来代替上图中的 stack/ queue 从而实现一种自定义的遍历方式。

例如可以使用一个随机容器（随机队列），通过对边的随机性访问来生成一个随机迷宫

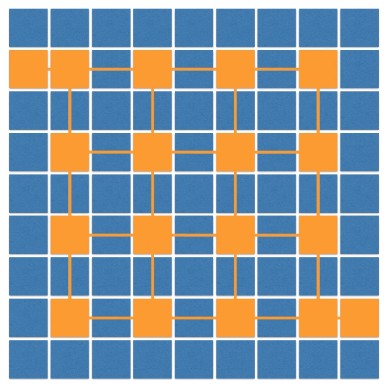
更大更好看的例子：

6. 图论问题建模和 floodfill (DFS)

LeetCode 图论算法练习：

785. 判断二分图

可以参考 Section 4.4

java 实现：LeetCode785_me.java（作者使用了BFS）

695. 岛屿的最大面积

该问题的核心为图的建模，也就是从题目所给的二维数组中提取点、边的信息。我们的目标是把如下矩阵

[[0,0,1,0,0,0,0,1,0,0,0,0,0],
 [0,0,0,0,0,0,0,1,1,1,0,0,0],
 [0,1,1,0,1,0,0,0,0,0,0,0,0],
 [0,1,0,0,1,1,0,0,1,0,1,0,0],
 [0,1,0,0,1,1,0,0,1,1,1,0,0],
 [0,0,0,0,0,0,0,0,0,0,1,0,0],
 [0,0,0,0,0,0,0,1,1,1,0,0,0],
 [0,0,0,0,0,0,0,1,1,0,0,0,0]]

转化成

// AdjList[i] 储存结点i的邻接点
AdjList = [[1, 4, 8], [2, 7, 9], ...]

但传统邻接表内结点的表示为整数，而在题干矩阵中，结点则以二维位置参数表示，主要步骤如下：

（1）将结点信息由二维映射至一维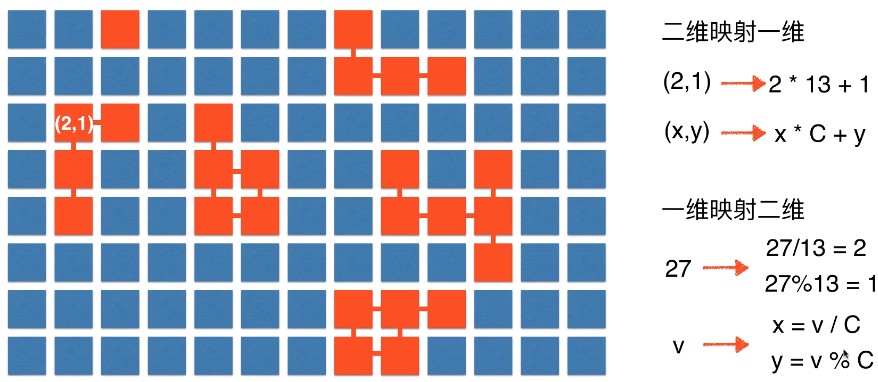

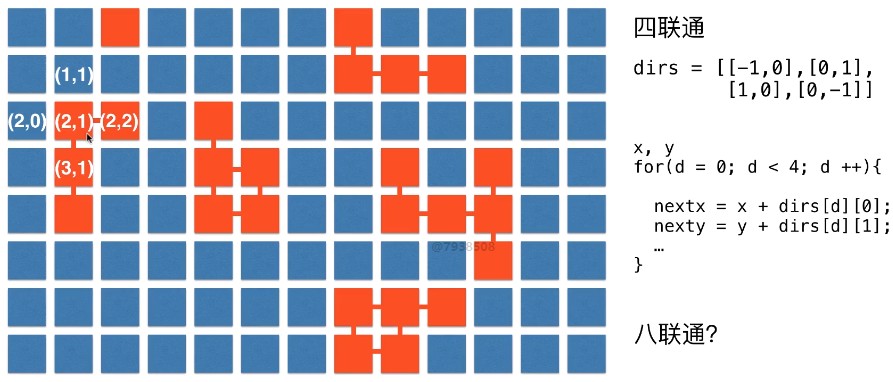
（2）判断任一结点是否存在相邻点

（3）根据之前写的求解无向图联通分量的算法，完成代码主体

可以参考 Section 4.1

java 实现 v1：LeetCode695_me.java（LeetCode 上显示我击败了5.3%的用户…，好垃圾。可能是使用了一些相对复杂的数据结构，但是在逻辑方面我个人感觉还是挺OK的） java 实现 v2：LeetCode695.java（更好的代码示例）先将二维矩阵转化为 HashSet 类型的图信息，再使用 dfs。核心代码：

private int[][] dirs = { {-1, 0}, {0, 1}, {1, 0}, {0, -1} }; // 四连通

private HashSet<Integer>[] constructGraph(){
    HashSet<Integer>[] g = new HashSet[R * C];
    for (int i = 0; i < g.length; i++)
        g[i] = new HashSet<>();

    for (int v = 0; v < g.length; v++) {
        int x = v / C, y = v % C; // 将一维信息转化为二维坐标
        if (grid[x][y] == 1) {
            for (int d = 0; d < 4; d++) {
                int nextx = x + dirs[d][0], nexty = y + dirs[d][1];
                if (inArea(nextx, nexty) && grid[nextx][nexty] == 1){
                    int next = nextx * C + nexty;
                    g[v].add(next);
                }}}}
    return g;
}

private int dfs(int v){
    visited[v] = true;
    int res = 1;
    for(int w: G[v]){
        if(!visited[w])
            res += dfs(w);
    }
    return res;
}

java 实现 v3：LeetCode695_plus.java 直接使用输入的二维矩阵来保存图信息，改造 dfs 使之适用于二维输入。核心代码：

private int dfs(int x, int y){
    visited[x][y] = true;
    int res = 1;
    for(int d = 0; d < 4; d++){
        int nextx = x + dirs[d][0], nexty = y + dirs[d][1];
        if(inArea(nextx, nexty) && !visited[nextx][nexty] && grid[nextx][nexty] == 1)
            res += dfs(nextx, nexty);
    }
    return res;
}

6.1 floodfill 算法

上一个小节的最后一段代码（java 实现 v3）也被称之为 floodfill 算法，本质上与 dfs 相同，只不过将原本的根据边来传播的方式，更改为在坐标系内向的四个方向的传播。图例如下：

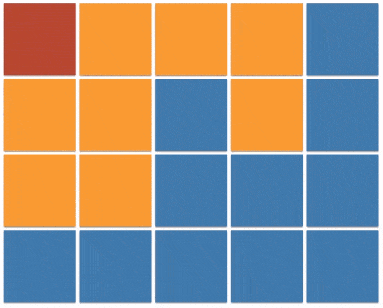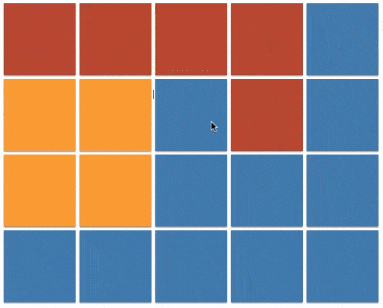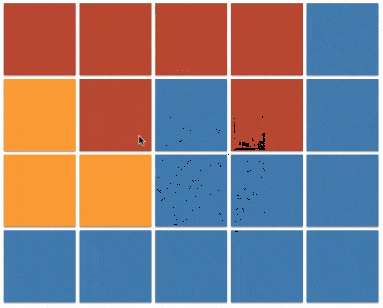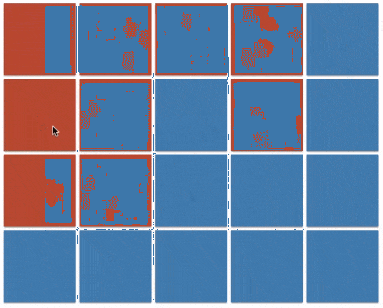
floodfill 的应用

ps里边的魔棒、扫雷游戏

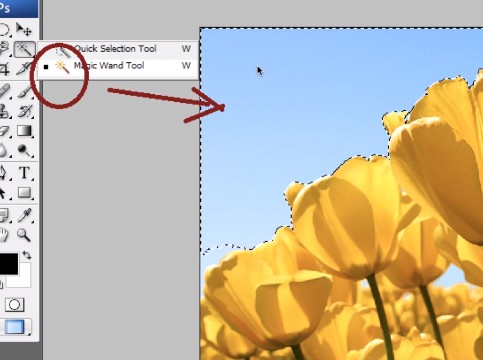
LeetCode 中的相关问题

200. 岛屿的数量 1020. 飞地的数量 130. 被围绕的区域 733. 图像渲染（floodfill） 1034. 边框着色 529. 扫雷游戏 827. 最大人工岛屿 [Hard]

6.2 连通性和并查集

class UF{
    private int[] parent;

    public UF(int n){
        parent = new int[n];
        for(int i = 0 ; i < n ; i ++)
            parent[i] = i;
    }

    public int find(int p){
        if( p != parent[p] )
            parent[p] = find( parent[p] );
        return parent[p];
    }

    public boolean isConnected(int p , int q){
        return find(p) == find(q);
    }

    public void unionElements(int p, int q){
        int pRoot = find(p);
        int qRoot = find(q);
        if( pRoot == qRoot )
            return;
        parent[pRoot] = qRoot;
    }
}

以下将以图 + 代码结合的方式展示并查集的创建、运行过程：

UF uf = new UF(6);

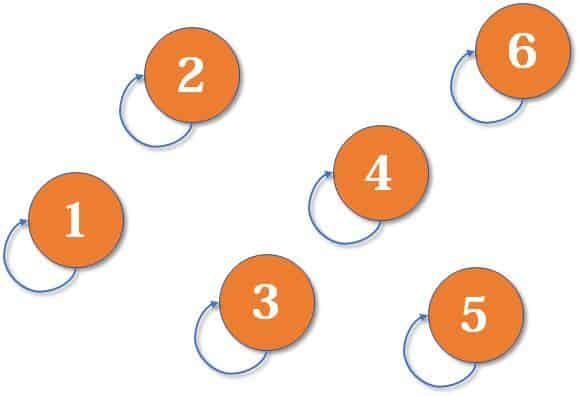
uf.unionElements(2, 1);
uf.unionElements(3, 1);
uf.unionElements(5, 4);
uf.unionElements(6, 4);

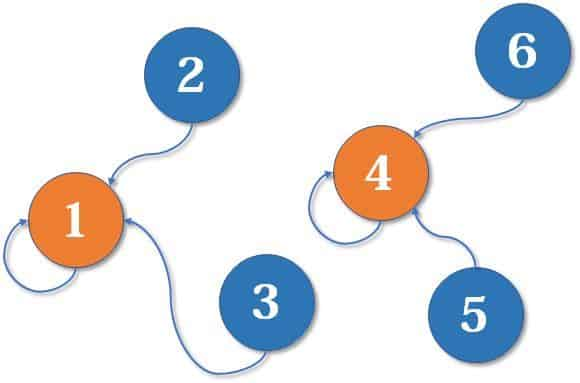
uf.unionElements(4, 1);

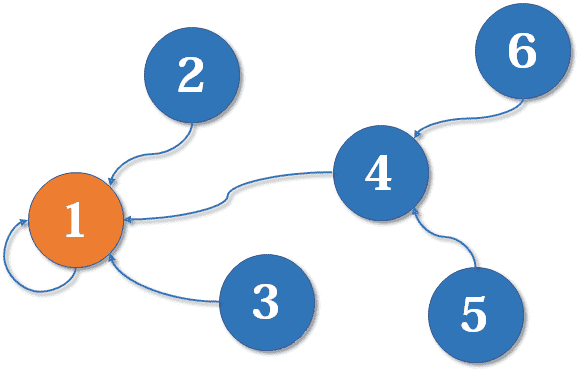
需要注意的是函数 `find(int p)`，该函数在每次运行的时候不仅仅能返回结点p的根节点，还将结点p的父结点直接改成其根结点。这样的功能实现能够避免出现长长一大串的连接

更进一步的，我们可以改进 UF 类，使之支持查找任意一元素所在集合的元素个数

class UF{
    private int[] parent;
    private int[] sz; // 1. 我们需要一个 sz 数组，存储以第 i 个元素为根节点的集合的元素个数。

    public UF(int n){
        parent = new int[n];
        sz = new int[n];
        for(int i = 0 ; i < n ; i ++){
            parent[i] = i;
            sz[i] = 1; // 2. 初始化，每个 sz[i] = 1
        }
    }

    public int find(int p){ // 没有变化... }
    public boolean isConnected(int p , int q){ // 没有变化 }

    public void unionElements(int p, int q){
        int pRoot = find(p);
        int qRoot = find(q);
        if( pRoot == qRoot )
            return;
        parent[pRoot] = qRoot;
        // 3. 维护 sz：把 qRoot 的集合元素数量加上 pRoot 的集合元素数量
        sz[qRoot] += sz[pRoot];
    }

    // 4. 最后，设计一个接口让用户可以查询到任意一个元素 p 所在的集合的元素个数 
    public int size(int p){
        return sz[find(p)]; // 使用 p 所在的集合的根节点查找相应的元素个数
    }
}

使用 floodfill + 并查集的 LeetCode 练习

695. 岛屿的最大面积

7. 图论搜索和人工智能 (BFS)

1091. 二进制矩阵中的最短路径

这道题与 Section 6 中介绍过的 695. 岛屿的最大面积非常相似，区别在于 1091. 使用了 BFS 而不是 DFS（BFS 能帮助求解无向无权图的最短路径）

java 实现 v1：LeetCode1091_me.java（因为有了之前写 695. 的经验，这道题写得比较满意，在没有刻意追求空间与速度的情况下仍能 > 75%）

java 实现 v2：LeetCode1091.java 这两种实现方式的区别仅仅在于 v1 使用一维数组来存储距离信息 length 和访问信息 visited，而 v2 使用二维数组

7.1 图论建模的核心：状态表达（752. 打开转盘锁为例）

想要使用图论的方法解决一道算法题，核心是尝试分析能否找到问题中所隐含的“点”、“边”

以 LeetCode 752. 打开转盘锁为例：

该题中的， “点”：指代任意转盘锁的状态，例如 0000 “边”：描述了转盘锁从原本的状态转到下一个状态的过程，例如从 0000 有八条边连接八种状态

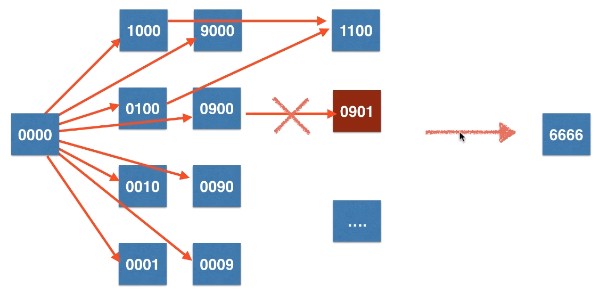
通过这样的转换，我们发现其实这道题和之前在 Section 6、7 中所遇到的 695.、1091. 挺相似的，区别在于这道题的结点不是一种类似坐标那样真实存在，而是一种“状态”

java 实现 v1：LeetCode752_me.java（我使用了数字索引的方式，将输入的 string 全部转化为 int 后处理，结果用时击败 5%，内存消耗击败 99%）

java 实现 v2：LeetCode752.java 注意下列代码 while 中的第一个 for 循环，使用取余的方式实现了 0 与 9 之间的转换

public int openLock(String[] deadends, String target) {
    HashSet<String> deadset = new HashSet<>();
    for(String s: deadends) deadset.add(s);

    // 初始的条件判断...略

    // 储存访问信息：只要包含在 visited 的 keys() 中即为已访问
    // 储存距离信息：使用键值对映射的方式
    HashMap<String, Integer> visited = new HashMap<>();

    // BFS
    Queue<String> queue = new LinkedList<>();
    queue.add("0000");
    visited.put("0000", 0);
    while(!queue.isEmpty()){
        String curs = queue.remove();
        char[] curarray = curs.toCharArray();
        ArrayList<String> nexts = new ArrayList<>();
        for (int i = 0; i < 4; i++) {
            char o = curarray[i];
            // char 转 int 的方式
            curarray[i] = Character.forDigit((curarray[i] - '0' + 1) % 10, 10);
            nexts.add(new String(curarray));
            curarray[i] = o; // 把变更的数字还原
            // 这里没有使用 -1 是为了防止出现负数，+9 的效果等同于 -1，这类似与钟表原理
            curarray[i] = Character.forDigit((curarray[i] - '0' + 9) % 10, 10);
            nexts.add(new String(curarray));
            curarray[i] = o;
        }
        for(String next: nexts) {
            if (!deadset.contains(next) && !visited.containsKey(next)) {
                queue.add(next);
                visited.put(next, visited.get(curs) + 1);
                if (next.equals(target))
                    return visited.get(next);
            }
        }
    }
    return -1;
}

7.2 智力题：水桶倒水

只要问题中包含状态转移的需求，我们就可以尝试使用图论的方法

Question: 有两个水桶，一个最多能装5升，另一个3升。

只能进行如下操作：

把一个水桶的水倒光
把一个水桶的水灌满
把一个水桶里的的水倒到另一个水桶里，倒水的过程中不能有水溢出（例如A桶5L，B桶2L，那么A只能倒出1L水给B）

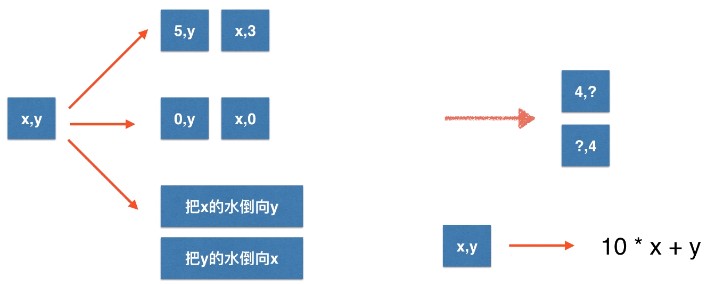
那么最少要几个步骤才能使任一水桶中有四升水？这个步骤具体是怎么倒的？

问题分析

把两个水桶在任意时刻内装的水量视为状态，那么倒水的过程就是一种状态转移（可以把这两者分别视为一个“图”中的“点”与“边”）

水桶的状态可以很容易地用一个十位数字来描述，因此问题的关键就在于如何描述这种状态转移的过程，核心代码如下：

public ArrayList<Integer> nextStates(int n){
    ArrayList<Integer> nexts = new ArrayList<>();
    int v1 = n / 10;
    int v2 = n % 10;
    // 加满一桶水
    if(v1 != 5) nexts.add(50 + v2);
    if(v2 != 3) nexts.add(v1 * 10 + 3);
    // 倒掉一桶水
    if(v1 != 0) nexts.add(v2);
    if(v2 != 0) nexts.add(v1 * 10);
    // 把 v1 的水倒进 v2
    if(v1 != 0){
        int dv = Math.min(v1, 3 - v2);
        nexts.add((v1-dv)*10 + (v2+dv));
    }
    // 把 v2 的水倒进 v1
    if(v2 != 0){
        int dv = Math.min(v2, 5 - v1);
        nexts.add((v1+dv)*10 + (v2-dv));
    }
    return nexts;
}

其余部分近似于 Section 4.2 中的求两点间路径的问题，需要定义一个 pre[] 数组来储存“路径”

java 实现：WaterPuzzle.java

773. 滑动谜题

根据题目可以得出以下信息：

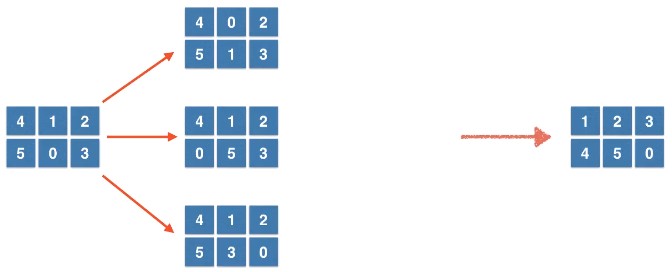
这道题和 Section 7.2 （752. 打开转盘锁为例）非常类似

java 实现 v1：LeetCCode773_me.java java 实现 v2：LeetCode773.java

7.3 图论搜索和人工智能

在这个 Section 里边的所有问题的解决方法，其实都是一种基于搜索的人工智能的体现（这里的人工智能 != 机器学习）

8. 桥、割点、图的遍历树

8.1 桥

定义

对于无向图，如果一条边的删除会导致整个图连通分量的数量变化，则这条边称为桥

桥意味着图中最脆弱的关系

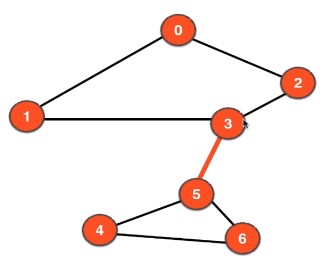
8.1.1 寻找桥的算法（DFS+）

算法使用的框架为 DFS，主要关注遍历边的过程：

如何判断 v-w 是不是桥

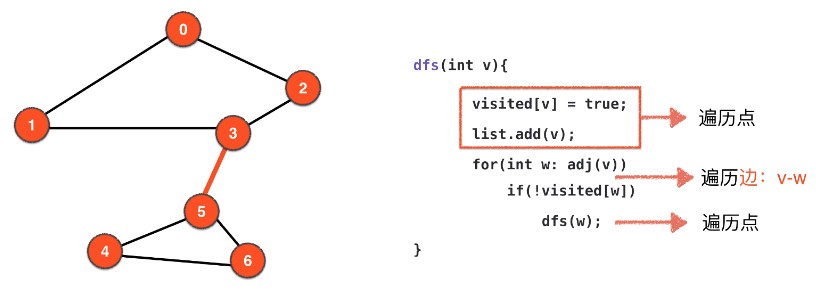
看通过 w，能否从另外一条路回到 v 或者 v 之前的顶点

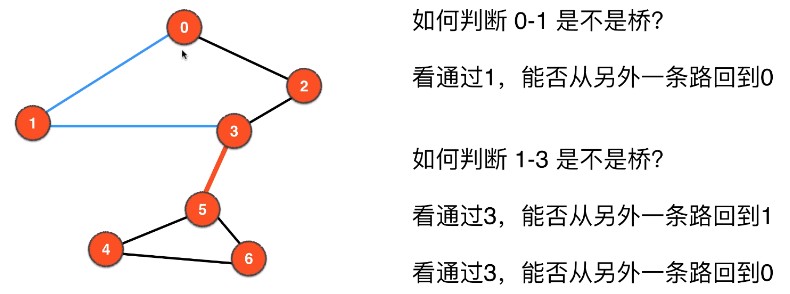
因此对于每一个顶点，我们需要记录 DFS 的顺序，例如使用 ord[v] 表示顶点 v 在 DFS 的访问顺序，ord[v] = 5 表示顶点 v 是第五个被访问到的顶点。

Document Information

Author: Zeka Lee
Link: https://zhekaili.github.io/0011/02/01/(Java)Graph-Theory-Basic/
Copyright: 自由转载-非商用-非衍生-保持署名（创意共享3.0许可证）

Zeka's Blog

Graph and Network Basic

1. Classifications

1.1 Undirected vs Directed

1.2 完全图、二分图

2. Basic Concepts

3. Representations of Graph

3.1 邻接矩阵

3.2 邻接表

3.3 比较：矩阵 vs 两种表

4. DFS (Deep-first Search)

4.1 Ex: 求联通分量

4.2 Ex: 求两点间路径

4.3 Ex: 环检测

4.4 Ex: 二分图检测

5. BFS (Breath-first Search)

5.1 Ex: 求两点间路径

5.2 性质：无权图最短路径

5.3 比较：DFS vs. BFS

6. 图论问题建模和 floodfill (DFS)

785. 判断二分图

695. 岛屿的最大面积

6.1 floodfill 算法

6.2 连通性和并查集

7. 图论搜索和人工智能 (BFS)

1091. 二进制矩阵中的最短路径

7.1 图论建模的核心：状态表达（752. 打开转盘锁为例）

7.2 智力题：水桶倒水

773. 滑动谜题

7.3 图论搜索和人工智能

8. 桥、割点、图的遍历树

8.1 桥

8.1.1 寻找桥的算法（DFS+）

Document Information

Search

Table of Contents