使用 C 实现
1. Abstract
数据元素 $D={a1, a2, …, an}$ 关系 $S={<a_i,a_{i+1}>\vert i=1,…,n-1}$ 基本操作:
InitList()返回一个初始化的空表ListLength(L)计算元素个数GetData(L, i)访问第i个元素InsList(*L, i, e)在第i个元素前插入值为e的元素DelList(*L, i, e)删除第i哥元素,其值存在e中被返回Locate(L, e)查找元素e的位置,找到返回序号,找不到返回0DestroyList(L)销毁表ClearList(*L)清空表IfEmptly(L)判断是否为空
graph LR
A(线性表)
A-->B1(顺序存储结构)
A-->B2(链式存储结构)
B2--->C21(单链表)
B2--->C22(循环链表)
B2--->C23(双向循环链表)
B2--->C24(静态链表)
2. 线性表(顺序存储)
线性表的顺序存储结构可以借助一维数组来表示
2.1 定义
点击查看代码
```c #define SIZE 100 typedef int ElemType; // 数据结构的定义 typedef struct{ ElemType elem[SIZE]; // 占用的数组空间 int last; // 最后一个元素的下标值,空表为-1 }SeqList; // 初始化 SeqList *InitList( ){ SeqList *p; p = (SeqList *)malloc(sizeof(SeqList)); p->last = -1; return p; } // 查找(按内容) int Locate(SeqList *L, ElemType e){ for(int i=0; i <= L->last; i++){ if (L->elem[i]==e) return i+1; } return -1; } // 查找(按序号) ElemType GetData(SeqList *L, int i){ if(i <= L->last+1){ return L->elem[i-1]; }else{ printf("Wrong number"); return NULL; } } // 插值 int InsList(SeqList *L, int i, ElemType e){ if((i<1) || (i>L->last+2)){ printf("插入位置%d不合法", i); return -1; }else if(L->last >= SIZE-1){ printf("表已满无法继续插入"); return -1; }else{ for(int k=L->last; k>=i-1; k--){ L->elem[k+1] = L->elem[k]; } L->elem[i-1] = e; L->last++; return 1; } } // 删除 //TODO: 这里的代码有问题,会产生EXC_BAD_ACCESS int DelList(SeqList *L, int i, ElemType *e){ if((i<1) || (i>L->last+1)){ printf("删除位置%d不合法", i); return -1; }else{ *e = L->elem[i-1]; // 该语句会报错 for(int k=i; i <= L->last; k++){ L->elem[k-1] = L->elem[k]; } L->last--; return 1; } } ```2.2 应用示例:合并表
将两个升序排列的表合并成一个同样升序排列的新表
点击查看代码
```c SeqList *MergeList(SeqList *L1, SeqList *L2){ int i=0, j=0, k=0; SeqList *L3; L3 = InitList(); while(i <= L1->last && j <= L2->last){ if(L1->elem[i] <= L2->elem[j]){ L3->elem[k++] = L1->elem[i++]; }else{ L3->elem[k++] = L2->elem[j++]; } } while(i <= L1->last){ L3->elem[k++] = L1->elem[i++]; } while(j <= L2->last){ L3->elem[k++] = L2->elem[j++]; } L3->last = L1->last + L2->last + 1; return L3; } void main(){ SeqList *p1; p1 = InitList(); for(int i=0; i<10; i++) InsList(p1, i+1, i+50); SeqList *p2; p2 = InitList(); for(int i=0; i<10; i++) InsList(p2, i+1, i+45); SeqList *p3 = MergeList(p1, p2); for(int i=0; i<=p3->last; i++) printf("%4d", p3->elem[i]); } ```2.3 优缺点
Pros:
- 无需为表示结点元素之间的逻辑关系而额外增加存储空间
- 读取元素 $O(1)$
Cons:
- 插入/删除元素 $O(n)$
- 预先分配存储空间,不适用于表长变化大的情况
3. 线性表(链式存储)
每个数据结点包含两个域:
- 数据域存储结点的值
- 指针域存储指向后继结点的指针
为了操作方便,一般在单链表的第一个结点之前设置一个头结点,其数据域可以存放诸如链表长度之类的信息,而其指针域存储指向第一个结点的指针
3.1 定义
两种链表的创建方式:从头部插入 or 从尾部插入 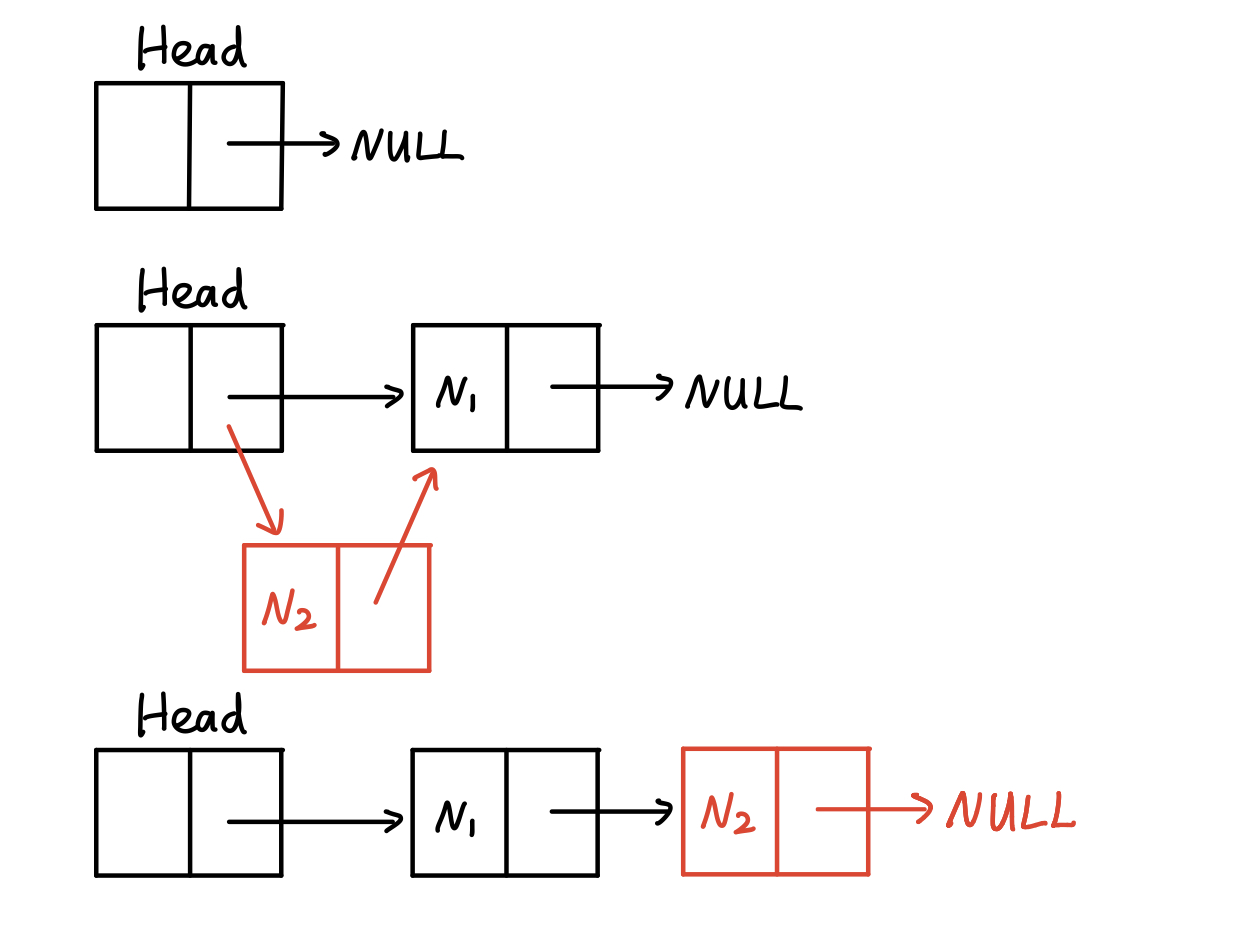
点击查看代码
```c typedef char ElemType; typedef struct{ ElemType data; struct Node *next; }Node, *LinkedList; // 初始化单链表 void InitLL(LinkedList *L){ // 传入一个二级指针(指向头结点) // 为一级指针(头结点)分配一个地址,并将二级指针指向一级指针 *L = (Node *)malloc(sizeof(Node)); (*L)->next = NULL; } // 创建结点:从头部插入(链表顺序与输入顺序相反) // 示例:输入"abc$",使用 PrintLL() 后的输出结果为"c-->b-->a" void CreateFromHead(LinkedList L){ Node *s; char c; while(1){ c = getchar(); // 当输入'$'时,循环终止 if(c != '$'){ s = (Node *)malloc(sizeof(Node)); s->data = c; s->next = L->next; L->next = s; }else break; } } // 创建结点:从尾部插入(链表顺序与输入顺序相同) // 示例:输入"abc$",使用 PrintLL() 后的输出结果为"a-->b-->c" void CreateFromTail(LinkedList L){ Node *last = L; Node *s; char c; while(1){ c = getchar(); // 当输入'$'时,循环终止 if(c != '$'){ s = (Node *)malloc(sizeof(Node)); s->data = c; s->next = NULL; last->next = s; last = s; }else break; } } // 打印单链表 void PrintLL(LinkedList L){ Node *n = L->next; // 由头结点访问第一个结点 while(n->next != NULL){ printf("%c-->", n->data); n = n->next; } printf("%c\n", n->data); // 打印尾结点 } // 按位置查找:查找第i个结点 Node *Get(LinkedList L, int i){ Node *n = L; int j = 0; while((n->next != NULL) && (j<i)){ n = n->next; j++; } if(i == j) return n; else return NULL; } // 按数值查找:查找值为e的结点 Node *Locate(LinkedList L, ElemType e){ Node *n = L; while(n->next != NULL){ n = n->next; if(e == n->data) return n; } return n->next; // 找不到时,n->next == NULL } // 链表长度 int LengthLL(LinkedList L){ Node *n = L; int len = 0; while(n->next != NULL){ n = n->next; len++; } return len; } // 插入结点,在位置i插入值e int InsList(LinkedList L, int i, ElemType e){ Node *pre = L; int j = 0; while((pre->next != NULL) && (j<i-1)){ pre = pre->next; j++; } if(!pre->next){ printf("插入位置不合理\n"); return -1; } Node *n; n = (Node *)malloc(sizeof(Node)); n->data = e; n->next = pre->next; pre->next = n; return 1; } // 删除结点,删除i位置的结点并将其数值返回 ElemType DelList(LinkedList L, int i){ Node *pre = L; int j = 0; while((pre->next != NULL) && (j<i-1)){ pre = pre->next; j++; } if(!pre->next){ printf("插入位置不合理\n"); return '\0'; } Node *n = pre->next; pre->next = n->next; return n->data; } ```3.2 应用示例:合并链表
将两个升序排列的链表合并成一个同样升序排列的新链表
点击查看代码
```c LinkedList MergeLL(LinkedList L1, LinkedList L2){ LinkedList L3; InitLL(&L3); Node *n3; n3 = L3; Node *n1 = L1->next; Node *n2 = L2->next; while((n1 != NULL) && (n2 != NULL)){ if(n1->data <= n2->data){ n3->next = n1; n3 = n1; n1 = n1->next; }else{ n3->next = n2; n3 = n2; n2 = n2->next; } } // n1不为NULL说明L1末尾还有几项没并入L3,直接通过指针完成合并 if(n1 != NULL) n3->next = n1; else n3->next = n2; return L3; } void main(){ LinkedList l1, l2, l3; InitLL(&l1); CreateFromTail(l1); PrintLL(l1); InitLL(&l2); CreateFromTail(l2); PrintLL(l2); l3 = MergeLL(l1, l2); PrintLL(l3); } ```4. 循环单链表
循环单链表的表尾结点指向表头结点
4.1 定义
可以通过两种方式定义循环单链表
- 以头结点地址代表整个链表(近似于单链表)
- 以尾结点地址代表整个链表,这种方法的优势在于,可以很容易地把两个循环单链表拼起来
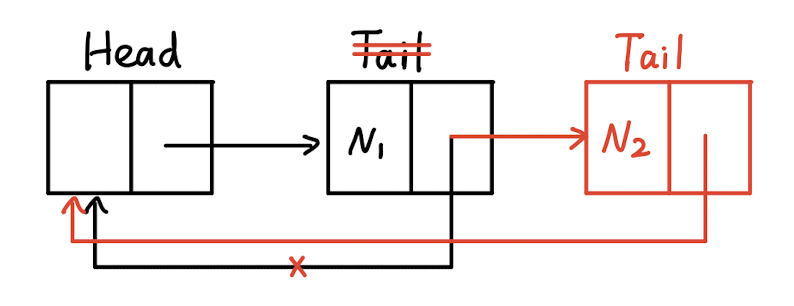
4.1.1 方式一: 头结点代表
注意 MergeCL() 函数,其中使用了两个while循环,$O(n)$
点击查看代码
```c typedef char ElemType; typedef struct{ ElemType data; struct Node *next; }Node, *LinkedList; // 初始化循环单链表 void InitCL(LinkedList *CL){ // 传入一个二级指针(指向头结点) // 为一级指针(头结点)分配一个地址,并将二级指针指向一级指针 *CL = (Node *)malloc(sizeof(Node)); (*CL)->next = (*CL); } // 创建结点:从尾部插入(链表顺序与输入顺序相同) // 示例:输入"abc$",使用 PrintCL() 后的输出结果为"a-->b-->c-->a" void CreateCL(LinkedList CL){ Node *s, *rear; // 尾结点rear rear = CL; // 初始状态下头结点 = 尾结点 char c; while(1){ c = getchar(); // 当输入'$'时,循环终止 if(c != '$'){ s = (Node *)malloc(sizeof(Node)); s->data = c; rear->next = s; rear = s; }else break; } rear->next = CL; // 把尾结点rear指向头结点 } // 打印循环单链表 void PrintCL(LinkedList L){ Node *n = L->next; // 由头结点访问第一个结点 while(n != L){ // 当n不为头结点时,循环打印 printf("%c-->", n->data); n = n->next; } n = n->next; // 循环结束后n为头结点,因此需要再赋值一次以访问第一个结点 printf("%c\n", n->data); // 打印第一个结点,表示链表的循环 } LinkedList MergeCL(LinkedList L1, LinkedList L2){ Node *n1 = L1->next; Node *n2 = L2->next; while (n1->next != L1) n1=n1->next; // L1的尾结点 while (n2->next != L2) n2=n2->next; // L2的尾结点 n1->next = L2->next; // L1的尾结点连接L2的第一个结点 n2->next = L1; // L2的尾结点连接L1的头结点 free(L2); return L1; } void main(){ LinkedList cl1, cl2, cl3; InitCL(&cl1); CreateCL(cl1); PrintCL(cl1); InitCL(&cl2); CreateCL(cl2); PrintCL(cl2); cl3 = MergeCL(cl1, cl2); PrintCL(cl3); } ```4.1.2 方式二: 尾结点代表
这里的 MergeCL() 为 $O(1)$
点击查看代码
```c // 创建循环单链表结点:从尾部插入(链表顺序与输入顺序相同) LinkedList CreateCL(LinkedList CL){ Node *s, *rear; // 尾结点rear rear = CL; // 初始状态下头结点 = 尾结点 char c; while(1){ c = getchar(); // 当输入'$'时,循环终止 if(c != '$'){ s = (Node *)malloc(sizeof(Node)); s->data = c; rear->next = s; rear = s; }else break; } rear->next = CL; // 把尾结点rear指向头结点 return rear; // 返回尾结点代表循环单列表 } // 打印循环单链表 void PrintCL(LinkedList L){ Node *n = L->next; // 由尾结点访问头结点 n = n->next; // 再访问第一个结点 while(n != L->next){ // 当n不为头结点时,循环打印 printf("%c-->", n->data); n = n->next; } n = n->next; // 循环结束后n为头结点,因此需要再赋值一次以访问第一个结点 printf("%c\n", n->data); // 打印第一个结点,表示链表的循环 } LinkedList MergeCL(LinkedList L1, LinkedList L2){ Node *head1 = L1->next; Node *head2 = L2->next; L1->next = head2->next; // L1的尾结点连接到L2的第一个结点 L2->next = head1; // L2的尾结点连接到L1的头结点 return rear2; } void main(){ LinkedList cl1, cl2, cl3; InitCL(&cl1); cl1 = CreateCL(cl1); PrintCL(cl1); InitCL(&cl2); cl2 = CreateCL(cl2); PrintCL(cl2); cl3 = MergeCL(cl1, cl2); PrintCL(cl3); } ```5. 双向循环链表
5.1 定义
双向循环列表的每个结点都包含三个元素:
- prior 指针指向前一个元素的地址
- data 储存值
- next 指针指向后一个元素的地址
下图展示了一个空的双向循环链表的结构,以及插值的过程 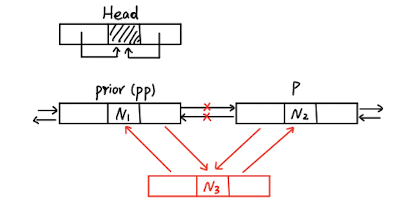
在删除结点的过程中,需要按如下顺序执行,如果先执行步骤2 (p->next)->prior = p->prior,那么之后 p->prior 将变得无意义,最终使得步骤1 (p->prior)->next = (p->next) 无法执行 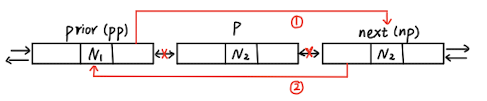
点击查看代码
```c typedef char ElemType; typedef struct{ ElemType data; struct Node *prior, *next; }DNode, *DoubleList; // 初始化双向循环链表 void InitDL(DoubleList *DL){ // 传入一个二级指针(指向头结点) // 为一级指针(头结点)分配一个地址,并将二级指针指向一级指针 *DL = (DNode *)malloc(sizeof(DNode)); (*DL)->prior = (*DL); (*DL)->next = (*DL); } // 创建双向链表结点:从头部插入(链表顺序与输入顺序相反) void CreateDL(DoubleList DL){ DNode *s, *p, *pp; // 尾结点rear char c; while(1){ c = getchar(); // 当输入'$'时,循环终止 if(c != '$'){ s = (DNode *)malloc(sizeof(DNode)); s->data = c; // 以下代码实现在p结点前插入s结点,pp = p->prior // pp&p 都可以用DL化简掉,这里是为了增强代码可读性 pp = DL; p = DL->next; s->prior = pp; pp->next = s; s->next = p; p->prior = s; }else break; } } int DLinkInsert(DoubleList DL, int i, ElemType e){ DNode *s, *p, *pp; int k=0; p = DL; while((p->next != DL) && (k < i)){ p = p->next; k++; } if(k!=i){ printf("插入位置不合适"); return -1; } pp = p->prior; s = (DNode *)malloc(sizeof(DNode)); s->data = e; s->prior = pp; pp->next = s; s->next = p; p->prior = s; return 1; } ElemType DLinkDelete(DoubleList DL, int i){ DNode *p, *pp, *np; // Node p, prior pp, next np int k=0; p = DL; while((p->next != DL) && (k < i)){ p = p->next; k++; } if(k!=i){ printf("删除位置不合适"); return '\0'; } pp = p->prior; np = p->next; pp->next = np; np->prior = pp; ElemType deldata = p->data; free(p); return deldata; } // 打印双向循环链表 void PrintDL(DoubleList DL){ DNode *n = DL->next; // 由头结点访问第一个结点 while(n != DL){ // 当n不为首结点时,循环打印 printf("%c<-->", n->data); n = n->next; } n = n->next; // 循环结束后n为首结点,因此需要再赋值一次以访问第一个结点 printf("%c\n", n->data); // 打印第一个结点,表示链表的循环 } void main(){ DoubleList dl1; InitDL(&dl1); CreateDL(dl1); PrintDL(dl1); DLinkInsert(dl1, 3, 'e'); PrintDL(dl1); ß ElemType deldata = DLinkDelete(dl1, 3); PrintDL(dl1); printf("Deleted data: %c\n", deldata); } ```6. 静态链表
静态链表即模拟链表,实现:
- 用数组
StaticList[]模拟内存 - 用数组下标
cursor模拟指针,头结点的cursor为0,尾结点为-1 - 编写从数组中分配和回收结点的方法
6.1 定义
6.1.1 静态链表的创建、插入结点与删除结点
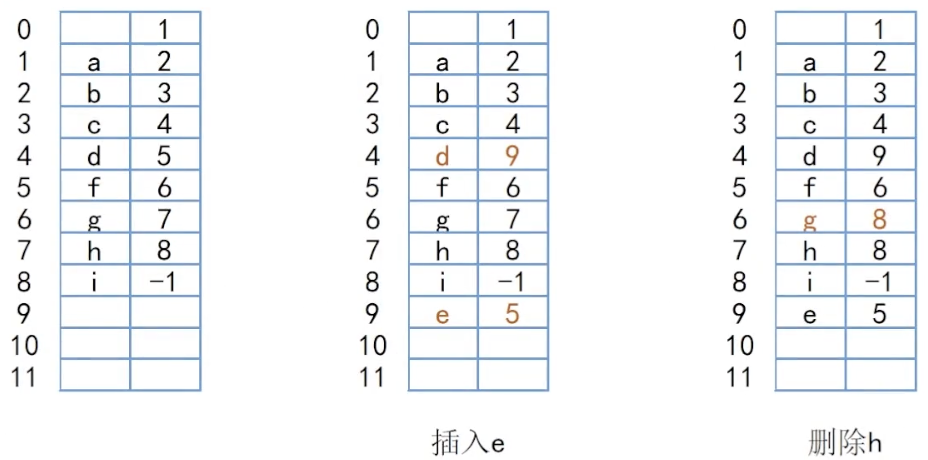
上图中的删除操作并不完整,因为结点 StaticList[6] 虽然被删除但没有被回收,也就是说我们在之后的需要按如下顺序执行插入操作中无法定位到这个结点</span>,这会导致静态链表在多次插入删除操作之后“假满”
解决方式:创建一个“空闲链表”连接所有未被分配存储空间的结点以及因删除操作而回收的结点
6.1.2 链表的初始化
- 头结点为尾结点:
StaticList[0].cursor = -1 - 初始化”空闲链表“,并创建一个头指针指向该链表的第一个元素

void InitSL(StaticList space, int *av){
space[0].cursor = -1;
// 建立"空闲链表"
for(int k=1; k<SIZE-1; k++){
space[k].cursor = k+1;
}
space[SIZE-1].cursor = -1; // 标记尾链
*av = 1; // "空闲链表"的头指针
}
6.1.3 结点空间的分配和回收
// 分配结点
int getNode(StaticList space, int *av){
int i = *av;
*av = space[*av].cursor;
return i;
}
// 回收结点
void freeNode(StaticList space, int *av, int k){
space[k].cursor = *av;
*av = k;
}
其他函数类似于单链表
6. 小结
几种操作结构总结 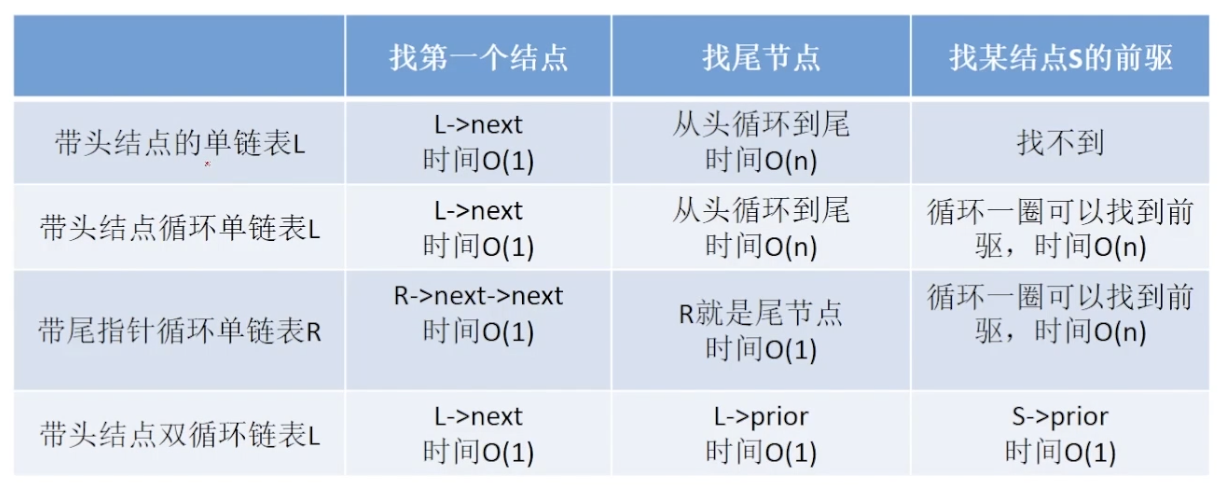
Document Information
- Author: Zeka Lee
- Link: https://zhekaili.github.io/0011/03/01/(C)Linear-List/
- Copyright: 自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)