1. Merge Sort

1.1 伪代码 & 时间复杂度分析

def mergeSort(arr [length=n]):
    L = mergeSort(1st half of arr) [length=n/2]
    R = mergeSort(2nd half of arr) [length=n/2]
    i = 0 # 1
    j = 0 # 2
    for k = 0 to n-1:
        if L[i] < B[j]:
            arr[k] = L[i] # 3
            i++           # 4
        else:
            arr[k] = R[j] # 5
            j++           # 6

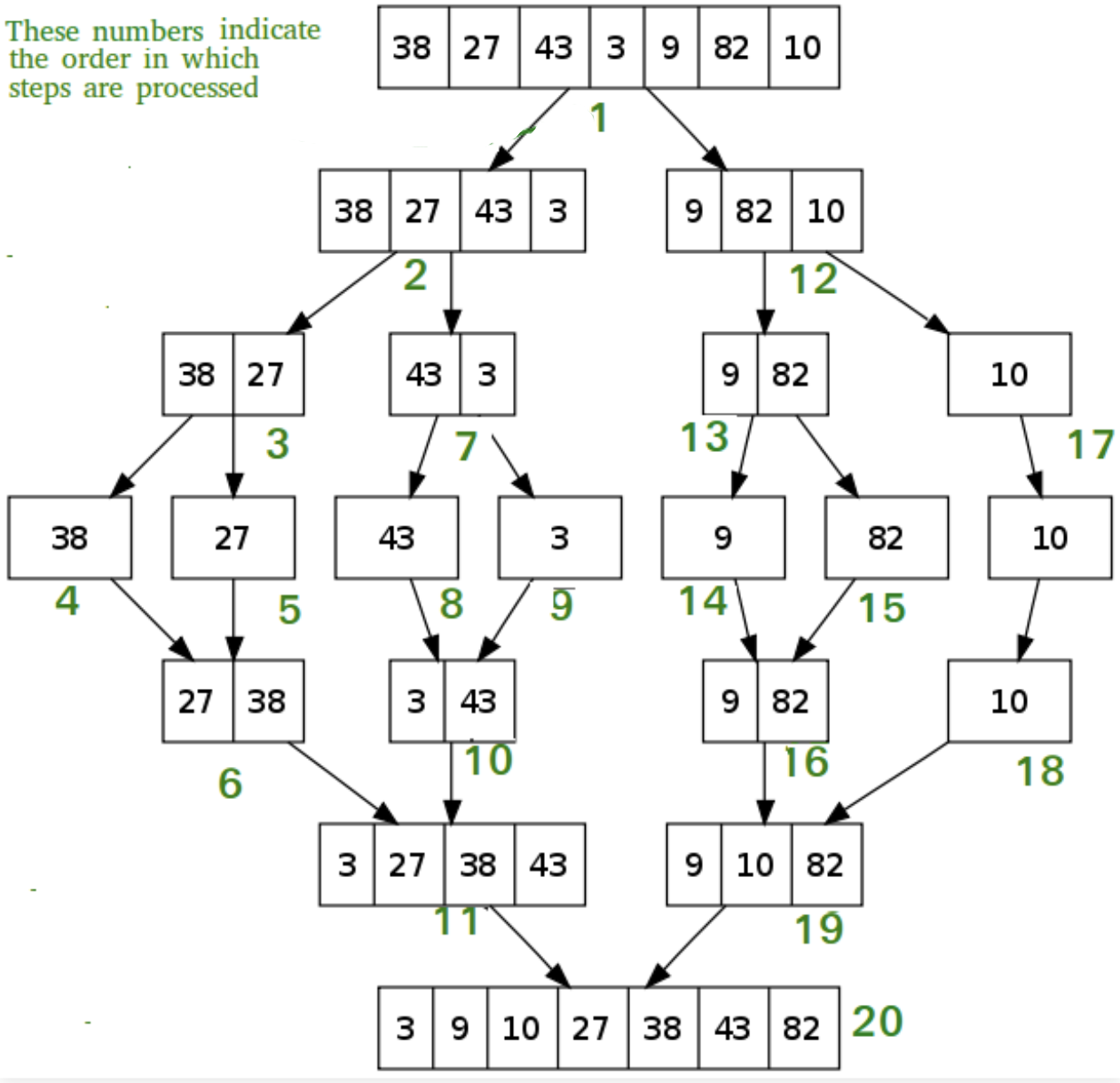
如树图的上半部分所示，一个长度为 $n$ 的数组可以拆分到 $\log_2n$ 层（原数组本身在第零层，因此共有 $\log_2n+1$ 层)。其中第 $j$ 层包含了 $2^j$ 个长度为 $n/2^j$ 的子列表

对于每个子列表均需要执行一次递归函数。如伪代码所示，每次运行将步骤1,2执行1次，步骤3,4,5,6执行n次（仅将赋值/运算过程作为考虑对象）

因此，函数每次运行的步骤数为： \(\text{steps per func}\leq 2+4n\leq 6n\)

第 $j$ 层包含的步骤数为： \(\text{steps of layer j}\leq 2^j\times 6(\frac{n}{2^j})=6n\)

总步骤数为（时间复杂度 $O(n\log_2n)$）： \(\text{steps overall}\leq 6n(\log_2n+1)\)

1.2 递归实现（Python）

理解递归的核心在于“假设”。而该算法的的 “假设” 为：递归函数 mergeSort(arr) 已经能够将 arr 正确排序

因此在对输入列表进行第一次二分切割后：

1. 使用 mergeSort(L | R) 表示分割后的两个子列表已经完成排序
2. 将这两个子列表合并为一个新的有序列表，并同时更新到 arr
3. 从而使得 arr 成为一个有序列表，这反过来证明了 “假设” 的正确性
4. 最后，还需要写出结束递归的信号（见第一行）

2. Asymptotic Analysis

Suppress constant factors and lower-order terms (used to get time complexity)

e.g. $6n\log_2n+5n\to O(n\log n)$

1. $6$ is a constant factor
2. $5n$ is a lower-order term

2.1 Big-Oh Notation

$T(n)=O(f(n))$ is valid iff there exist constants $c,n_0>0$ s.t. $T(n)\leq cf(n)$ for all $n\geq n_0$

2.2 Big-Omega Notation

Big-Oh is for upper-bound, while big-Omega is for lower-bound.

$T(n)=\Omega(f(n))$ is valid iff there exist constants $c,n_0>0$ s.t. $T(n)\geq cf(n)$ for all $n\geq n_0$

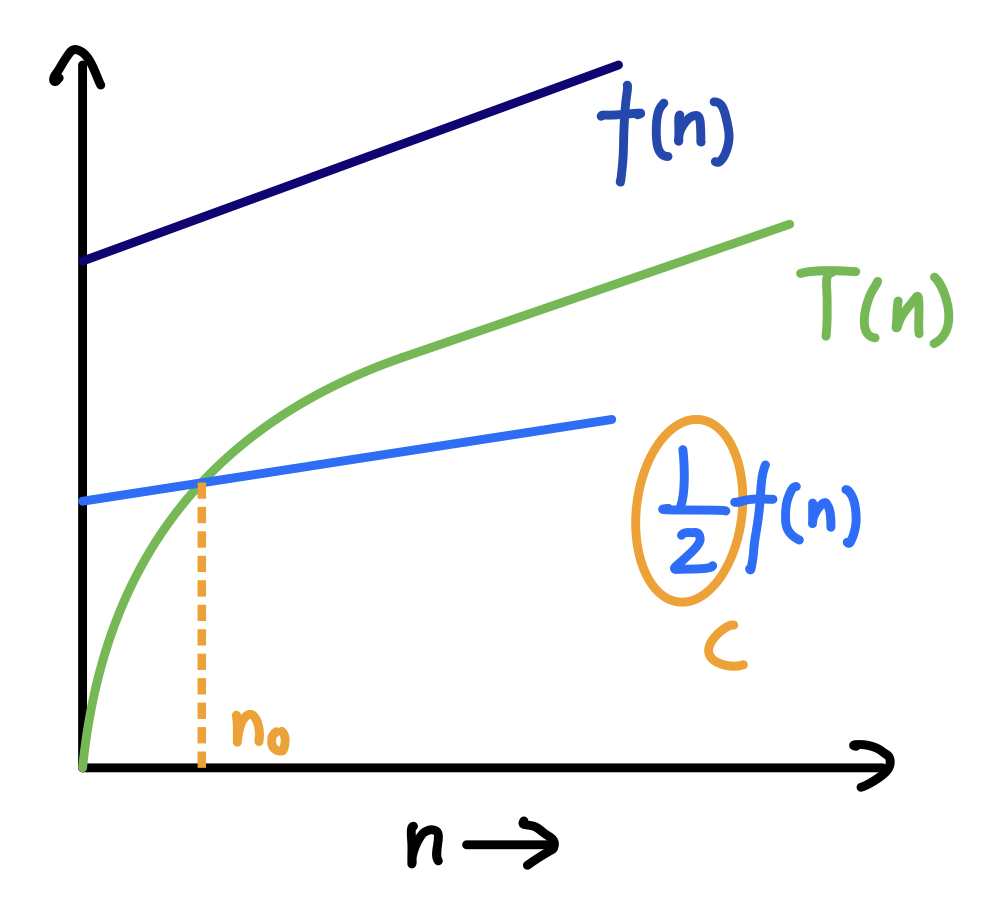
2.3 Big-Theta Notation

$T(n)=\Theta(f(n))$ is valid iff $T(n)=\Omega(f(n))$ and $T(n)=O(f(n))$

e.g. for function $T(n)=\frac{1}{2}n^2+3n$ $T(n)=O(n^3)$, $T(n)=\Theta(n^2)$, $T(n)=\Omega(n)$

2.4 Little-Oh Notation

$T(n)=o(f(n))$ is valid iff for all constant $c>0$, there exist constant $n_0>0$ s.t. $T(n)\leq cf(n)$ for all $n\geq n_0$

3. Divide & Conquer Algorithms

核心理念是由大割小，再执行小

3.1 Ex: Counting Inversions

目标：设计一个函数，对于输入数组 arr，查找所有满足 i<j 并且 rr[i]>arr[j] 的 pairs。例如 arr=[2,4,1,3] »> [(2,1),(4,1),(4,3)]

算法1: 遍历 $O(n^2)$

ans = []
for i in range(len(arr)):
    for j in range(i+1, len(arr)):
        if arr[i] > arr[j]: ans.append((arr[i], arr[j]))

算法2: Merge Inversion $O(n\log n)$

应用 Divide & Conquer 的核心理念，我们希望能通过拆分+递归的方式，实现对于时间复杂度的降低。类似于 Section1.Merge Sort 所使用的方法：

1. 把输入列表 arr 均分为左右两个子列表
2. 先分别求这两个子列表内所包含的 inversion pairs
3. 再求这两个子列表之间的 inversion paris（每一对中大的来自左列表，小的来自右列表）

def CountInv(arr): # 返回 inversion paris
    if len(arr) > 1:
        mid = len(arr) // 2
        LInv = CountInv(arr[:mid])
        RInv = CountInv(arr[mid:])
        SInv = CountSplitInv(arr)
        return LInv + SInv + RInv

以上函数就能实现上述步骤的思路框架，现在还差对函数 CountSplitInv() 的定义。这里同样借鉴 Section1.Merge Sort 的思路：

1. 若不操作，需嵌套遍历两子列表的所有元素，时间复杂度仍为 $O(n^2)$
2. 但如果分割后的两个子列表都已经是降序排列，只需要遍历一遍，即在 Merge 的同时若发现 L[i]>R[j]，则在返回值 inversions pairs 中添加 {(L[i], R[j_]) | for every j <= j_ < len(R)}，该方式的时间复杂度为 $O(n)$
3. 因此，函数 CountSplitInv() 除了需要能够返回 inversion pairs，还要能够将输入列表降序排列

def CountSplitInv(arr):
    ans = []
    if len(arr) > 1:
        mid = len(arr) // 2
        L = arr[:mid]
        R = arr[mid:]

        # ans1, ans2 没有用，这是为了接受函数输出
        # 运行完后 L, R 就都变成了降序排列
        ans1, ans2 = CountSplit(L), CountSplit(R)

        i = j = k = 0
        while i < len(L) and j < len(R):
            if L[i] < R[j]: 
                arr[k] = R[j]
                j++
            else: 
                arr[k] = L[i]
                for j_ in range(j, len(R)):
                    ans.append((L[i], R[j_]))
                i++
            k++
  
        while i < len(L): arr[k] = L[i], i++, k++
        while j < len(R): arr[k] = R[j], j++, k++

Python 实现：

3.2 Ex: Subcubis Matrix Multipliacation

两个矩阵之间相乘的复杂度为 $O(n^3)$

使用 Divide & Conquer 方法，先将两个输入矩阵切分成四块小矩阵，再将小矩阵相乘。该方法的复杂度仍为 $O(n^3)$（假设 $n=2^i$，且仅考虑乘法带来的复杂度问题）：

例如，一个$2\times 2$的矩阵可以被切分$1$次，每次切分需要做$8$个乘法，共执行$8^1=8$次。而一个$n\times n$的矩阵可被切分$\log_2n$次，因此共执行$8^{\log_2n}=2^{3\log_2n}=n^3$次

def subCubMult(M1, M2):
    if len(M1) > 1:
        M = np.zeros([len(M1), len(M1)])
        A1, B1, C1, D1 = upleft, upright, downleft, downright of M1
        A2, B2, C2, D2 = upleft, upright, downleft, downright of M2
        
        upleft of M    = subCubMult(A1, A2) + subCubMult(B1, C2)
        upright of M   = subCubMult(A1, B2) + subCubMult(B1, D2)
        downleft of M  = subCubMult(C1, A2) + subCubMult(D1, C2)
        downright of M = subCubMult(C1, B2) + subCubMult(D1, D2)
        return M
    else:
        return M1 * M2

Strassen’s Subcubic Matrix Multiplication Algorithm

该算法通过将每次切分时所需要做的乘法次数由$8$次降到$7$次，从而极大降低了矩阵乘法的时间复杂度： \(7^{\log_2n}\ll 8^{\log_2n}=n^3\)

4. The Master Method

The Master method is a general method for solving (getting a closed form solution to) recurrence relations that arise frequently in divide and conquer algorithms, which have the following form: \(T(n)=aT(\frac{n}{b})+O(n^d)\)

$T(n):$ maximum runtime with size $n$ $a,b,d:$ constants

• $a:$ number of recursive calls (>=1), 例如每次递归切成三块 (a=3)
• $b:$ shrinkage factor (>1)
• $d:$ runtime of “combine step”

4.1 Examples

Binary Search

• 每次二分之后仅需要对其中的一块进行 recurrence $a=1$
• 二分之后 size 减半 $b=2$
• 只需要对其中一个半区进行 recurrence $a=1$
• 只执行一次比较 $d=0$

因此 $1=2^0$, $T(n)=O(\log n)$

Merge Sort

• 每次二分之后需要对其中每块都进行 recurrence $a=2$
• 二分之后 size 减半 $b=2$
• merge 的过程是线性的 $d=1$

因此 $2=2^1$, $T(n)=O(n\log n)$

4.2 Proof

Assume that: \(T(n)\leq aT(\frac{n}{b})+cn^d\)

对 $T(n)$ 可以构建一个树状结构，其中第 $j$ 层包含 $a^j$ 个子结点，每个子结点的 size 为 $n/b^j$，因此： \(\text{Work at level }j\leq a^j\cdot c\Big(\frac{n}{b^j}\Big)^d=cn^d\cdot \Big(\frac{a}{b^d}\Big)^j\)

Therefore

• $a=b^d:$ 每层运行步骤数量不变，$T(n)\leq cn^d(\log_bn+1)$ $T(n)=O(n^d\log n)$
• $a\neq b^d:$ 由等比数列公式 $S_n=1+r^1+…+r^k=\frac{1-r^{k+1}}{1-r}$
• • $a<b^d:$ $r<1,S_n\leq\frac{1}{1-r}=\frac{1}{1-a/b^d}=\text{const}$ $T(n)=O(n^d)$
• • $a>b^d:$ $r>1,S_n\leq r^k=(\frac{a}{b^d})^{\log_bn}$ $T(n)\leq cn^d\frac{a^{\log_bn}}{n^d}=ca^{\log_bn}=cn^{\log_ba}$ $T(n)=O(n^{\log_ba})$

4.3 Tricks

使用 Master Method 解决其他形式的 T(n) 的复杂度问题

let $S(m)=T(2^m) = T(2^{m/2})+1=S(\frac{m}{2})+1$

for $S(m)=S(\frac{m}{2})+1$, we have $a=1,b=2,d=0$

then $S(m)=O(\log n)$

therefore $T(n)=S(\log n)=O(\log\log n)$

5. QuickSort Algorithm

快速排序算法：

1. 选择一个 pivot
2. 遍历列表中的其他所有元素，小的放在 pivot 右，大的放左
3. 对左右两个子列表重新进行以上两部操作

假设每次都选择第一个元素作为 pivot：

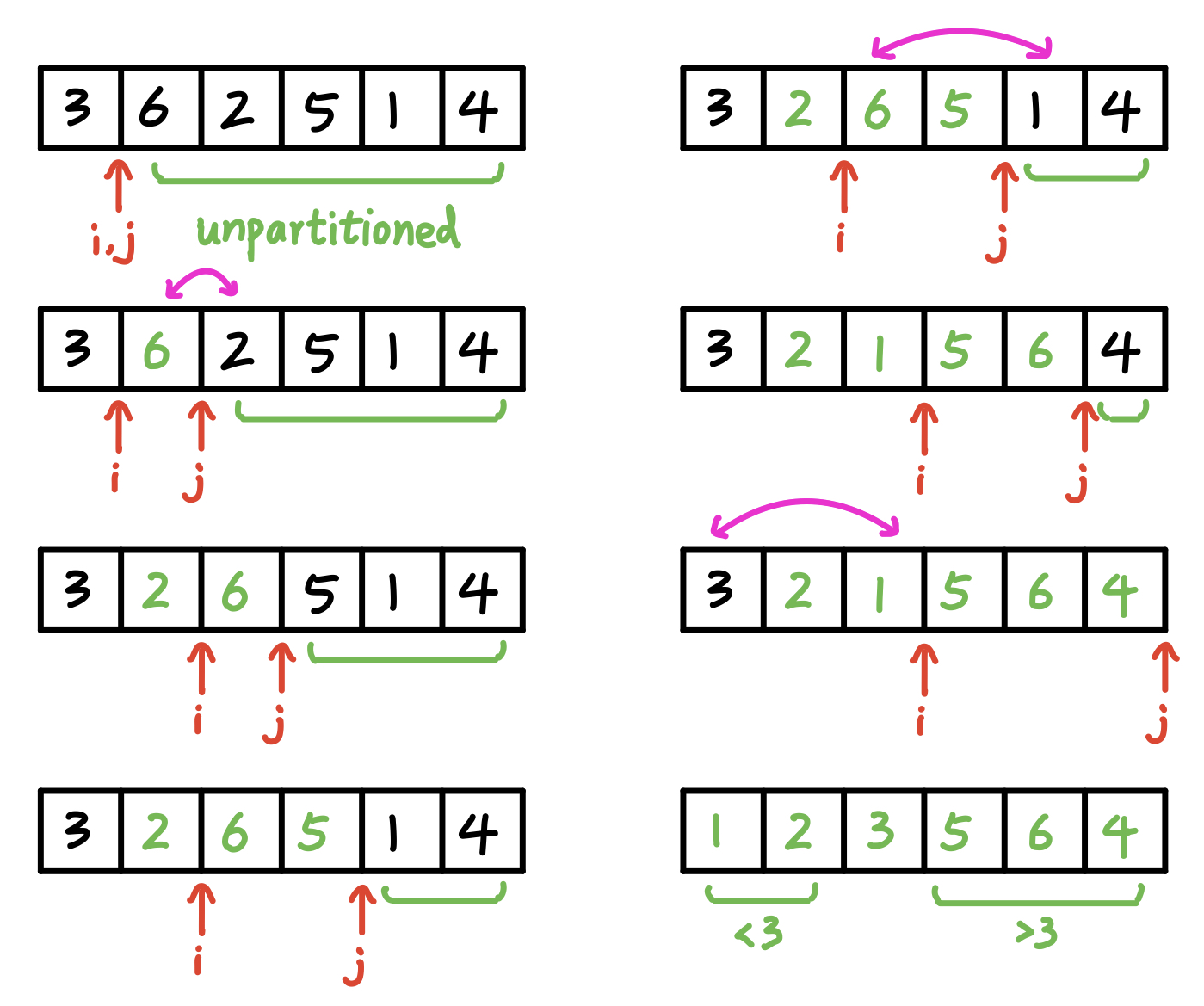
Python 实现：

def Partition(A, l, r):
    p = A[l]
    i = l+1
    for j in range(i, r+1):
        if A[j] < p:
            A[i],A[j] = A[j],A[i]
            i += 1
    A[l],A[i-1] = A[i-1],A[l]
    return i-1, i
    
def QuickSort(A, l, r):
    if r-l > 0:
        lr, rl = Partition(A, l, r)
        QuickSort(A, l, lr)
        QuickSort(A, rl, r)

存在的问题： 如果每次都选择第一个元素作为 pivot，那么在最坏的情况下（列表已经是一个有序列表），算法的时间复杂度为 $O(n^2)$

改进的方式可以是随机选择任一元素作为 pivot，在这种情况下平均的时间复杂度为 $O(n\log n)$，将在下一节予以证明

6. QuickSort Analysis

7. Probability Review