Python Basis

(1) copy() & deepcopy()

非常非常需要谨记的点！会容易造成很臭的 bug (1.1) X.copy()/ copy.copy(X) 浅拷贝: 即只拷贝第一层，第二层及以下的嵌套对象还是指向同一个地址

(1.2) copy.deepcopy(X) 深拷贝: 拷贝所有层级，每一层都是新的对象

从而我们可以得到以下结论:

对于单层且仅包含数值的 list, 使用 copy() or deepcopy()
对于多层且仅包含数值的 list, 使用 deepcopy()
对于单层但包含引用对象的 list, 例如，如果不想让对 L1 长度的修改影响到 L 和 L2；但又想让对 L1 中 obj1 的修改能够同步到 L 和 L2 中的 obj1，那么使用 copy()
```
L = [obj1, obj2]; L1 = L.copy(); L2 = L.copy()
```

常见的应用场景如下:

经常使用于函数接收输入的过程:

import copy()
class C1:
  def __init__(self, L=[], LL=[[]]):
    self.L = L.copy()
    self.LL = copy.deepcopy(LL)

列表的赋值过程: 我们希望从一个字典中读出一个列表，并在对该列表进行修改后，放进另一个字典中去

L = D1['L'].copy() # 这里是 copy or deepcopy 取决于 L 的内容，具体参考开头部分的结论
L = change(L)
D2['L'] = L

(2) `eval` 函数

eval 函数可以将字符串转换为 Python 代码并执行，例如:

eval('print("Hello World")')

当和 config.yaml 配合使用时，可以实现自定义执行任意函数，例如:

class_1:
  func_1: true
  func_2: false

c1 = Class_1()
for func in config['class_1']:
  if config['class_1'][func] == True:
    eval(f'c1.{func}()')

数据储存方式

(1) Reference in Stack Memory 栈（特点是后进先出，空间有限）储存所有对象名。执行方式类似于执行嵌套函数:

首先外部函数进入栈，然后内部函数入栈
内部函数执行完后先出栈，然后外部函数出栈

(2) Objects in Heap Memory 堆（特点是无序杂乱，空间大）储存所有创建的对象本身

1. Illustration

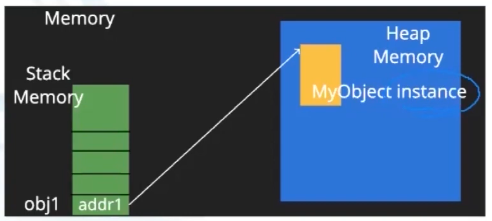
obj1 = MyObject()
id(obj1) >>> addr1

obj1 对象名(实例的reference)，储存在 stack memeory 中
MyObject() 实例(instance/ object)，储存在 heap memory 中
= 等号相当于创建了一个指针地址 address，将对象名指向实例。该地址和对象名一起储存在 stack memory 中
id(obj1) 读取对象名所储存的地址

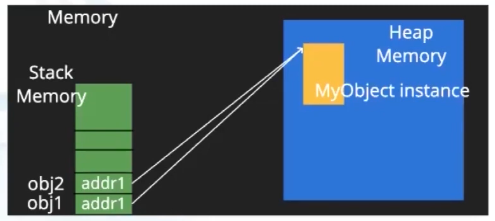
obj2 = obj1
obj1 is obj2 >>> True
id(obj1) == id(obj2) >>> True

把 obj1 对应的地址(addr1)赋给了 obj2，此时这两个对象名储存了同一个地址，因此指向同一实例对象

obj2 = MyObject()

又创建了一个新的实例对象，将其地址赋给 obj2
此时 obj1 is obj2 >>> False 因为指向不同实例对象
但是 obj1 == obj2 >>> True 因为他们指向的实例对象在属性值上相同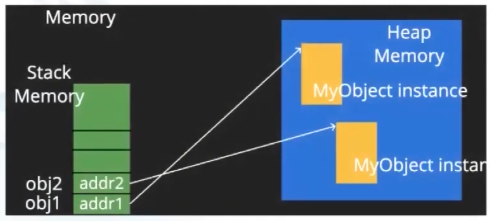

2. Examples

函数传参的本质是传递 object address。例如，下例中 F() 的执行过程相当于把 obj 对应的地址赋给 input

def F(input):
    input.a += 1

obj = MyObject()
obj.a = 4
F(obj)
print(obj.a) >>> 5

再例如对于数组

def F(lis):
  lis.append(1)
  lis = [2,3]

L = [0]
F(L)
print(L) >>> [0,1]

因此不管是在函数内部修改 class 的 fields 还是修改 list (list.append) 等等，都能够传递到函数外部，因为本质上是在修改实例对象

但如果在函数内部进行的是赋值操作，那就不会传递到函数外部

文件操作

开关
f = open(<文件名>, <打开模式>)
# 代码块
f.close()
|打开模式| 描述| |-|-| |’t’| 文本文件模式，只读，默认值| |’b’| 二进制文件模式，只读| |’r’| 只读，若文件不存在会报错| |’w’| 覆盖写入| |’x’| 创建写入，若文件存在则报错| |’a’| 追加写入| |’+’| 与r/w/x/a一同使用，在原功能基础上增加同时读写功能| |’wb’| 二进制覆盖写| |’…’| …|

读写 ```py
读
f.read(size) # 读入全部（可选参数：读取前size长度） f.readline(size) # 读入一行（可选参数：读取前size长度） f.readlines(hint) # 读入全部行，返回一个列表（可选参数：读取前hint行）

写

f.write(s) # 写入一个字符串或字节流 f.writelines(lines) # 写入一个字符串列表 f.seek(offset) # 改变文件操作指针的位置（0: 文件开头，1: 当前位置，2: 文件结尾）

例如：
```py
f.writelines(["aa", "bb"])
f.seek(0) # 不写这一行代码，该程序将不会输出任何内容
for line in f:
    print(line)
f.close()

>>>
"aabb"

函数

3.1 常用函数

enumerate(List)

L = [1,0]
for i, e in enumerate(L):
  print(i, e)
>>> 
0, 1
1, 0

eval() 执行并返回一个字符串表达式的值

a = eval("1 + 4")
b = eval("a * 6")

map(参数1, 参数2) 将参数1的方法作用于参数2得每一个元素

list(map(eval, ["1+1", "2*2"])) >>> [2, 4]

max(iterable, key=func) 使用 max + key 来发掘更多可用性

# 1. 统计列表中出现频率最高的元素
a = [1,2,3,1,2,3,2,2,4,5,1]
max(set(a), key=a.count) >>> 2

# 2. 求特定位置的最大值
lst = [(1,'a'), (3,'c'), (4,'e')]
max(lst, key=lambda x: x[0]) >>> (4, 'e')

3.2 lambda function

func = lambda [arg1, arg2, ...]: expression

Examples:

power = lambda a, b: a**b
power(2, 3) >>> 8

库

1. pip 命令

可以在 pypi.org 上根据关键字搜索第三方库

pip install <库名>
pip uninstall <库名>
pip install -U <库名> # 更新库
pip download <库名> # 下载但不安装
pip show <库名> # 查看库的详细信息
pip search <库名> # 检索与该库相关的信息

2. 构建自己的库

库名一般等于文件夹名，且文件夹中必须有一个 __init__.py 文件，该文件可以为空

2.1 库的结构

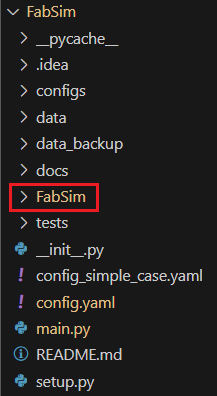
FabSim 库名文件夹
- __init__.py
- FabSim 主程序文件夹，一般同库名
  - __init__.py
  - components 组件程序文件夹
  - untils 工具程序文件夹
  - 以上仅为实例，实际情况可根据需要自行添加修改
- data
- docs
- tests
- config.yaml 配置文件
- main.py 主程序入口
- README.md
- setup.py 安装文件

2.2 `config.yaml` 配置文件

参考: https://docs.ansible.com/ansible/latest/reference_appendices/YAMLSyntax.html

配置文件以字典的形式储存程序运行所需的参数，从而使得用户可以通过修改配置文件来改变程序的运行方式，而不需要修改程序本身。

如下示例展示了如何定义和使用 .yaml 文件:

- martin:
    name: Martin D'vloper
    company: &SKWS Skyworks Solutions, Inc. # 定义一个锚点
    job: Developer
    skills:
      - python
      - java
- tabitha:
    name: Tabitha Bitumen
    compnay: *SKWS # 使用锚点(简单理解为引用变量)
    job: Developer
    skills:
      - SQL
      - Excel

import ruamel.yaml

with open(config_dir, 'r') as f:
  config = ruamel.yaml.safe_load(f)

print(config['martin']['name']) >>> "Martin D'vloper"
print(config['martin']['skills']) >>> ['python', 'java']
print(config['tabitha']['company']) >>> "Skyworks Solutions, Inc"

如果想要每次运行都保存一次配置文件，可以在程序中添加如下代码：

config['experiment_name'] = "new name"

with open("new_location.yaml", 'w') as f:
  ruamel.yaml.dump(config, f, Dumper=ruamel.yaml.RoundTripDumper)

类

class CS:
  def __init__(self, name):
    self.name = name

  # 定义 print(类对象) 时的输出值
  def __str__(self):
    print("Class: CS")
    return "Name: " + self.name

cs = CS("Tom")
print(cs)

>>>
Class: CS
Name: Tom

ipython in Jupyter

ipython 是一个交互式 shell，同时被应用于 Jupyter。有很多方便的魔法命令：

1. 自动补全 Tab

2. 执行终端命令 ! + 终端命令 例如 !ifconfig

3. 模糊查找 查找内容 + ? 例如 list_1.*pp*? 能查找目标对象所有名字中带有 pp 字段的方法/属性

4. 查看信息 对象/方法 + ? 例如 list_1?, list_1.append?

5. 查看函数代码 函数名 + ?? 例如 help?? 查看help函数的使用方法

6. 运行python程序 %run + 文件名.py

7. 使用前面代码块的输出结果 _ 前面第一个, __ 前面第二个, _n 序号为n的代码块：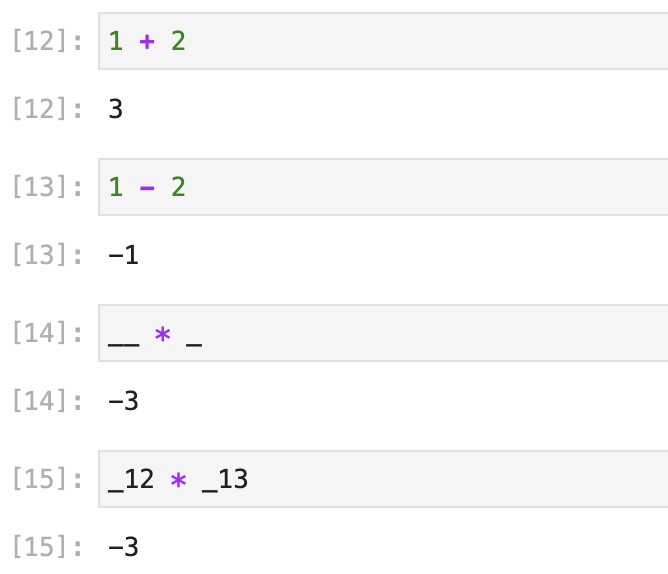

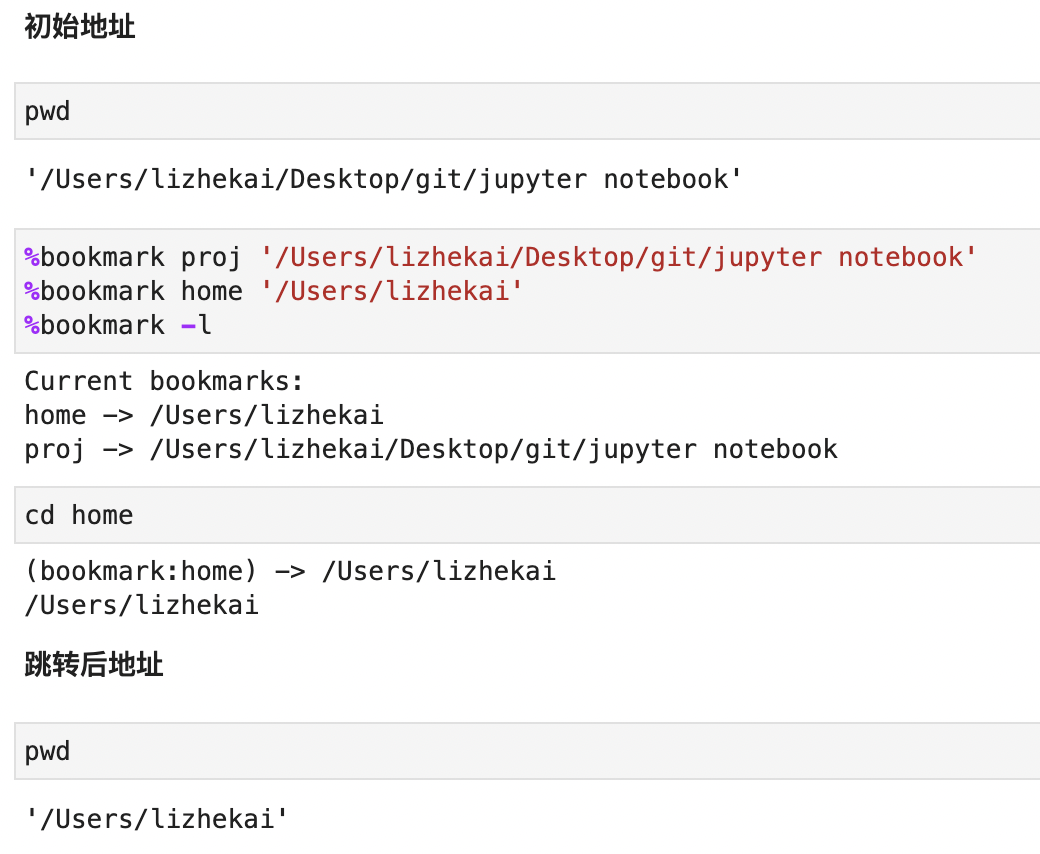
1. 为地址设置书签

设置书签 %bookmark 书签名地址 删除书签 %bookmark -d 书签名 删除所有书签 %bookmark -r 显示所有书签 %bookmark -l 跳转地址 cd 书签名

2. 代码调试

打开代码调试: %pdb on
之后如果运行错误代码，则会跳转到报错的前一行，并打开调试器，进入 pdb 调试模式，例如：
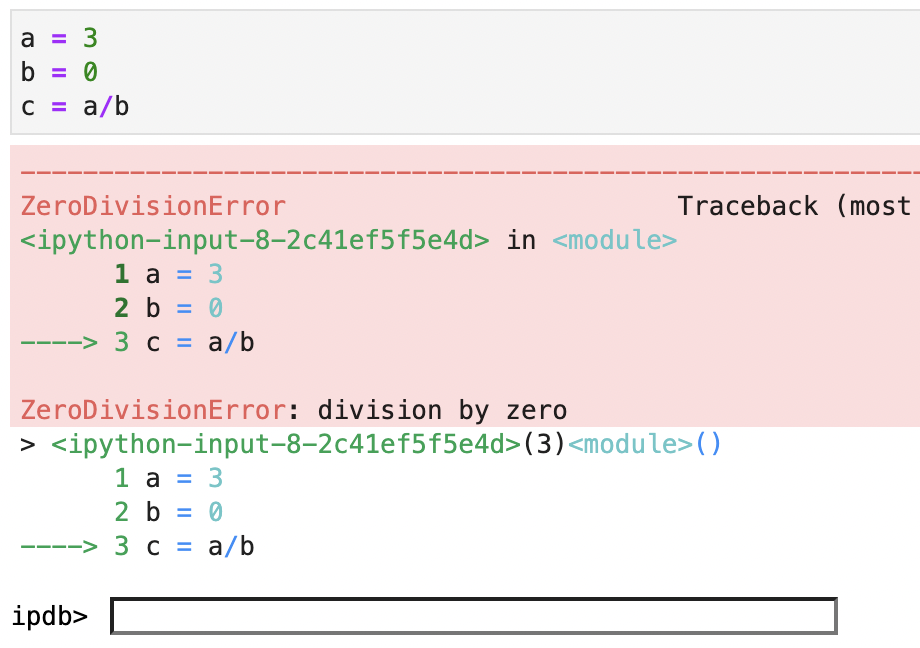
在调试器内输入调试命令，例如
```
p 变量名 # 查看变量值
```
退出调试: q(uit)

Time Complexity

6.1 Big O

$O$ usually used as Time Complexity notation. Understood as how run time or space requirements grow as the input size grows

Big O mathematically defined as the upper bound. 对于函数 $f(x)$，如果存在 $c\in\R$，使得 $f(x)<c\times g(x)$ 在其定义域内恒成立，则有 $f(x)\in O(g(x))$

例如，$N^3+8N+9<2(N^3)\implies O(N^3)$

6.2 Big Omega

$\Omega$ mathematically defined as the lower bound. 对于函数 $f(x)$，如果存在 $c\in\R$，使得 $f(x)>c\times g(x)$ 在其定义域内恒成立，则有 $f(x)\in\Omega(g(x))$

例如，$N^3+8N+9>0.5(N^3)\implies\Omega(N^3)$

6.3 Big Theta

$\theta$ uderstood as the exact performance value of the algorithm

Big Theta mathematically defined as both of the upper and lower bound i.e. if $f(x)\in O(g(x))$ and $f(x)\in\Omega(g(x))$ then $f(x)=\theta(g(x))$

虽然已经有了这些准确的定义，但我们在平常使用时只用 Big O（相当于 Big Theta）

6.4 Three Time Complexities

Best Case
Worst Case
Average Case

一般情况下，我们最关注的是时间复杂度的 Average Case，此外还需要关注 Worst Case（其重要性取决于具体情况，例如在安全工程领域很重要）

Ex: 对于快速排序 Quick Sort

Average Case: $O(n\log n)$
Worst Case: $O(n^2)$

6.5 Calculation

Program structure: How many times is basic calculation executed (e.g. for loop; while loop)
Master theorem: usually useful in recursive deduction
Mathematical deduction: Permutation, Combination, etc.
Mermorize common algorithms & data structures

6.5.1 Master theorem

\[T(n) = aT(\frac{n}{b}) + c*n^d\]

where $T(1)=d$. IF:

$\log_ba>d$, then $T(n)=O(n^{\log_ba})$
$\log_ba=d$, then $T(n)=O(n^d\log n)$
$\log_ba<d$, then $T(n)=O(n^d)$

如何理解这个公式呢？如下图:

$a=2$: branch factor 每次拆分时 branch 的个数
$b=3$: division factor 每次拆分时问题规模缩小的幅度
从 $T(n)\to T(1)$，共 $\log_bn$ 层

graph LR;
A["T(n)"];
B1["T(n/3)"]
B2["T(n/3)"]
C11["T(n/9)"]
C12["T(n/9)"]
C2["..."]
A --> B1
A --> B2
B1 --> C11
B1 --> C12
B2 --> C2

APPLICATIONs: 常用于 recursive deduction

Merge sort: $T(n)=2T(\frac{n}{2})+cn\implies O(n\log n)$
Binary search: $T(n)=T(\frac{n}{2})+c\implies O(\log n)$

但是有些递归推导式不适用于 master theorem，此时可以暴力推导

Selection sort: $T(n)=T(n-1)+cn\implies O(n^2)$ $T(n)=cn+c(n-1)+c(n-2)+…+c=n(n+1)/2$
Factorial: $T(n)=T(n-1)+c\implies O(n)$

6.5.2 Permutation, Combination

Permutation: 从 n 个人中挑选 k 个排成一列，有多少种挑选及排列方式

\[n\text{P}k=P(n,k)=\frac{n!}{(n-k)!}\]

Combination: 从 n 个人中挑选 k 个，有多少种挑选方式

\[n\text{C}k=C(n,k)=\frac{n!}{(n-k)!k!}\] \[C(n,k)=\frac{P(n,k)}{P(k,k)}\]

6.5.3 Memorize common algorithms & data structures

Binary search

Insertion sort, Binary sort, Selection sort, Quick sort, Merge sort

Binary tree, Binary search tree, Recursion, Hashtable (dictionary)

www.bigocheatsheet.com

Others

1. 星号(*)的使用

星号的作用为 unpacking: *实参，一般用于调用函数时

values = (1, 2)
sum(*values) >>> 3

a, *b = [1, 2, 3]
a >>> 1
b >>> [2, 3]

星号作为 packing: *形参, **形参，一般用于定义函数时

def func1(*args):
    print(args) # args is a tuple

def func2(**kwargs):
    print(kwargs) # kwargs is a dictionary

func1(1, 2, 3) >>> (1, 2, 3)
func2(a=1, b=2, c=3) >>> {'a': 1, 'b': 2, 'c': 3}

2. Eliminate Warnings

aka

取消 warning

import warnings
warnings.filterwarnings('ignore')

ask sam, todd, different dashboard, actually data

Document Information

Author: Zeka Lee
Link: https://zhekaili.github.io/wiki/python/python-basis/
Copyright: 自由转载-非商用-非衍生-保持署名（创意共享3.0许可证）

Zeka's Blog

Python - Basis

Python Basis

(1) copy() & deepcopy()

(2) `eval` 函数

数据储存方式

1. Illustration

2. Examples

文件操作

读

写

函数

3.1 常用函数

3.2 lambda function

库

1. pip 命令

2. 构建自己的库

2.1 库的结构

2.2 `config.yaml` 配置文件

类

ipython in Jupyter

1. 为地址设置书签

2. 代码调试

Time Complexity

6.1 Big O

6.2 Big Omega

6.3 Big Theta

6.4 Three Time Complexities

6.5 Calculation

6.5.1 Master theorem

6.5.2 Permutation, Combination

6.5.3 Memorize common algorithms & data structures

Others

1. 星号(*)的使用

2. Eliminate Warnings

Document Information

Search

Table of Contents

Python - Basis

Python Basis

(1) copy() & deepcopy()

(2) eval 函数

数据储存方式

1. Illustration

2. Examples

文件操作

读

写

函数

3.1 常用函数

3.2 lambda function

库

1. pip 命令

2. 构建自己的库

2.1 库的结构

2.2 config.yaml 配置文件

类

ipython in Jupyter

1. 为地址设置书签

2. 代码调试

Time Complexity

6.1 Big O

6.2 Big Omega

6.3 Big Theta

6.4 Three Time Complexities

6.5 Calculation

6.5.1 Master theorem

6.5.2 Permutation, Combination

6.5.3 Memorize common algorithms & data structures

Others

1. 星号(*)的使用

2. Eliminate Warnings

Document Information

Search

Table of Contents

(2) `eval` 函数

2.2 `config.yaml` 配置文件